Дипломная работа: Целочисленные функции
Спектр некоторого вещественного числа a определяется как бесконечное мультимножество целых чисел:
Spec (a ) = {![]() ,
, ![]() ,
, ![]() ,…} (10)
,…} (10)
Если ![]() , то Spec (a )¹Spec (b ), т.е. нет двух одинаковых спектров.
, то Spec (a )¹Spec (b ), т.е. нет двух одинаковых спектров.
Действительно, если предположить, что ![]() , то найдётся некоторое положительное целое число
, то найдётся некоторое положительное целое число ![]() , такое, что
, такое, что ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() . Таким образом, Spec(b ) содержит менее чем m элементов не больших
. Таким образом, Spec(b ) содержит менее чем m элементов не больших ![]() , тогда как Spec(α ) содержит по меньшей мере m .
, тогда как Spec(α ) содержит по меньшей мере m .
Пусть ![]() . Число элементов в Spec(
. Число элементов в Spec(![]() ), которые не превосходят
), которые не превосходят ![]() , равно
, равно
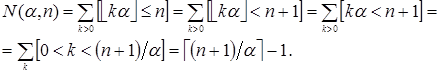 (11)
(11)
Говорят, что спектры образуют разбиение всех целых положительных чисел, если любое число, отсутствующее в одном спектре, присутствует в другом; но никакое число не содержится одновременно в обоих. Пусть ![]() и
и ![]() — вещественные положительные числа, тогда Spec(
— вещественные положительные числа, тогда Spec(![]() ) и Spec(
) и Spec(![]() ) образуют разбиение натуральных чисел тогда и только тогда, когда
) образуют разбиение натуральных чисел тогда и только тогда, когда ![]() . Интересное свойство спектров будет доказано в задаче 10. В задаче 17 будет показана связь между мультимножествами Spec(
. Интересное свойство спектров будет доказано в задаче 10. В задаче 17 будет показана связь между мультимножествами Spec(![]() ) и Spec
) и Spec![]()
![]() , где
, где ![]() — некоторое положительное число.
— некоторое положительное число.
V. ‘Mod’: бинарная операция.
Если m и n — целые положительные числа, то неполное частное от деления n на m равно ![]() . Для того, чтобы было удобно работать с остатками, введём определение остатка:
. Для того, чтобы было удобно работать с остатками, введём определение остатка:
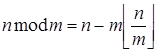 .
.
Это определение можно распространить на произвольные вещественные числа:
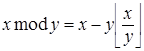 (12)
(12)
при ![]() . Положим
. Положим ![]() .
.
Дробную часть числа x можно представить как ![]() .
.
Самым важным алгебраическим свойством операции ‘mod’ является распределительный закон:
![]() (13)
(13)
Доказательство следует из (11):
![]() .
.
Приложение операции ‘ mod ’: разложение n предметов на m групп как можно более равномерных. Решение этого вопроса даёт тождества, справедливые при целых ![]() и натуральных
и натуральных ![]() .
.
![]() — выражает разбиение n на m как можно более равных частей в невозрастающем порядке. (14)
— выражает разбиение n на m как можно более равных частей в невозрастающем порядке. (14)
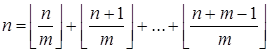 — выражает разбиение n на m как можно более равных частей в неубывающем порядке. (15)
— выражает разбиение n на m как можно более равных частей в неубывающем порядке. (15)
Доказательство этих фактов можно найти в книге Р.Грэхем, Д.Кнут, О.Паташник «Конкретная математика» на с.106-108. Если в (15) заменить n на ëmx ûи применить правило (8), то получим тождество, которое справедливо при любом вещественном x и натуральном ![]() :
:
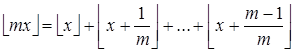 (16)
(16)
Глава 2. Целочисленные функции (применение к решению задач)
Задача 1.
Всякое натуральное число представимо в виде: ![]() , где
, где ![]() . Приведите явные формулы для l и m как функций от n .
. Приведите явные формулы для l и m как функций от n .
Решение:
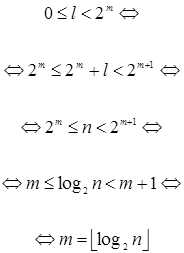
![]()
Тогда ![]()
Ответ: ![]() ,
, ![]() .
.
Задача 2.
Как выглядит формула для ближайшего целого к заданному вещественному числуx ? В случае «равновесия» — когда x лежит ровно посередине между целыми числами — приведите выражение, округляющее результат:
a) в сторону увеличения, т.е. до éx ù;
b) в сторону уменьшения, т.е. до ëx û.
Решение:
Пусть вещественное число ![]() округляется до
округляется до ![]() .
.
a) В этом случае до ![]() округляются числа
округляются числа ![]() , удовлетворяющие неравенству:
, удовлетворяющие неравенству:
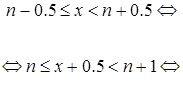
Û![]() (по свойству (4)).
(по свойству (4)).
b) В этом случае до ![]() округляются числа
округляются числа ![]() , удовлетворяющие неравенству:
, удовлетворяющие неравенству:
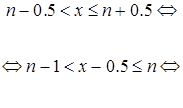
Û![]() (по свойству (4)).
(по свойству (4)).