Дипломная работа: Целочисленные функции

Задача 12.

Имеется ли аналогичное (16) тождество, в котором вместо «полов» используются «потолки»?

Решение:

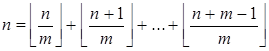Тождество (16) получается из тождества (15) заменой n на ëmx û.

Аналогичное тождество для потолков получается из тождества (14) заменой n на émx ù:

émx ù ==

==

Итак, получили тождество аналогичное данному:

émx ù =.

Задача 13.

Докажите, что . Найдите и докажите аналогичное выражение для вида , где ω – комплексное число .

Доказательство:

При делении числа на 2 возможны только два различных остатка: либо 0, либо 1.

· если , то и .

· если , и .

Следовательно, равенство верно для любого натурального n . Что и требовалось доказать.

Найдём аналогичное выражение для , т.е. найдём коэффициенты a , b , c .

Поскольку — есть корень третьей степени из 1, то и .

Так как , то .

При делении числа на 3 возможны только три различных остатка: либо 0, либо 1, либо 2.

Если , то .

Если , то .

Если , то .

Решая систему , находим a , b , c .

, , .

Итак, получаем следующую формулу:

.

Задача 14.

Какому необходимому и достаточному условию должно удовлетворять вещественное число , чтобы равенство выполнялось при любом вещественном ?

Решение:

При любом вещественном и равенство выполняется Ûb — целое число.

Еслиb — целое число, то функция непрерывная, возрастающая функция (так как ). Пусть — целое число, т.е. . Тогда , так как и . Выражая через , получим — целое, как натуральное число в неотрицательной целой степени. Поэтому можно применить формулу (6) и получить равенство .

Если b — не целое число, то при равенство не будет выполняться, так как