Дипломная работа: Упругопластическая деформация трубы

Второе условие – условие пластичности Мизеса-Генки – гласит, что пластические деформации в материале возникают, когда интенсивность касательных напряжений достигает некоторого постоянного для некоторого материала значения:

. (1.5.7)

Определим эту постоянную из результатов испытаний при простом растяжении. Подставляя в формулу

(1.5.8)

главные напряжения (1.5.1), найдем значение интенсивности касательных напряжений при растяжении в момент появления пластических деформаций:

. (1.5.9)

Сравнивая формулы (1.5.9) и (1.5.7), заключаем, что постоянная

. (1.5.10)

Подставляя выражения (1.5.8) и (1.5.10) в формулу (1.5.7), приходим к условию пластичности Губера-Мизеса-Генки в такой форме:

(1.5.11)

Или

.

Оба рассмотренных условия пластичности дают весьма близкие результаты. Эксперименты несколько лучше подтверждают условие Губера-Мизеса-Генки. Кроме того, это условие удобнее с математической точки зрения, так как выражение через шесть составляющих напряжений очень громоздко, а выражается через эти составляющие сравнительно просто. Поэтому в теории пластичности чаще используется условие пластичности Губера-Мизеса-Генки.

Ассоциированный закон

Пластические деформации возникают при активном нагружении материала и не возникают при нейтральном нагружении и разгрузке.

Соотношения связи в теории пластичности формулируется обычно на основе принципа максимума Мизеса: при фиксированных параметрах для любого данного значения компонент приращений пластической деформации имеет место неравенство

, (1.5.12)

где - действительные компоненты напряжения, а - компоненты любого возможного напряженного состояния, допускаемого данной функцией нагружения:

.

Из принципа максимума Мизеса следует ассоциированный закон течения – закон направленности приращения пластической деформации (или скорости пластической деформации) по градиенту к поверхности нагружения.

В самом деле, предположим, что приращение пластической деформации не зависит от приращения напряжений.

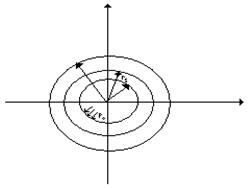
Рассмотрим рис. 1.7. Согласно (1.5.12) угол между векторами и должен быть не тупым. В силу произвольности вектора , не выходящего за поверхность нагружения , неравенство (1.5.12) может быть выполнено только в случае ортогональности к , откуда имеем

или

, , . (1.5.13)

Выражение (1.5.13) определяет ассоциированный закон пластического течения.

ГЛАВА II . ЗАДАЧА УПРУГОПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ТРУБЫ

2.1 Механическая постановка задачи

Рассмотрим упругопластическое состояние трубы радиусов , находящейся под действием внутреннего давления , в случае плоской деформации.