Дипломная работа: Упругопластическая деформация трубы
.
Получили дифференциальное уравнение:
.
Решим:
Из граничных условий (2.2.21) имеем
.
Тогда
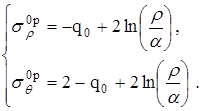(2.3.3)
Определим компоненты перемещений.
Из формул Коши (2.2.18) следует:
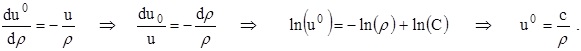
При 
из граничных условий (2.2.21) следует
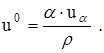
Упругость
Найдем компоненты деформации в упругой области 
.
Из закона Гука (2.2.20) вытекает
(2.3.4)
Формулы Коши (2.2.18) примут вид:
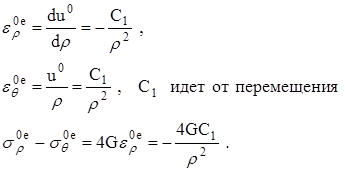
Из уравнений равновесий (2.2.17):
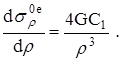
Решим:
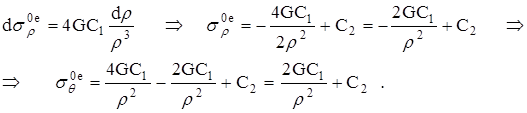
Из граничных условий (2.2.21) 
при
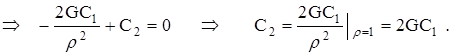
Тогда
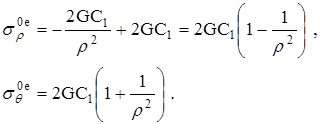(2.3.5)