Дипломная работа: Упругопластическая деформация трубы

Совершенно аналогично записываются выражения линеаризованных граничных условий для : чтобы получить линеаризованные граничные условия для , надо в (2.2.5) заменить на .

В линеаризованных задачах теории пластичности необходимо уметь записывать граничные условия (2.2.2) через компоненты основной системы координат. Для этого следует учесть угол поворота напряжений при переносе их на исходную окружность ().

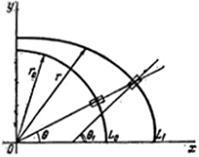
Рассмотрим рис 1.8. Угол , образован нормалью к контуру ;

- угол поворота напряжений при переносе их на исходный контур. Из известных формул теории упругости будем иметь

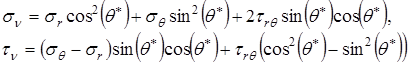(2.2.6)

Если уравнение границы тела записать в виде , то

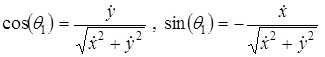(2.2.7)

Согласно (2.2.3) можно записать

(2.2.8)

Учитывая, что

(2.2.9)

Из (2.2.9), (2.2.7), (2.2.8) получим

(2.2.10)

Обозначая , найдем

(2.2.11)

(2.2.12)

Используя (2.2.1), (2.2.5), (2.2.6), (2.2.11), (2.2.12), получим искомые линеаризованные граничные условия: при должно иметь место

(2.2.13)

Перейдем к условиям сопряжения решений. На - границе упругой и пластической областей, должно иметь место

(2.2.14)

Уравнение контура запишется в виде

(2.2.15)

Учитывая разложение (2.2.1), подставляя в (2.2.14) выражение (2.2.15), получим исходное линеаризованное условие сопряжения. Очевидно, что условия сопряжения могут быть получены из (2.2.5), если заключить левые части в квадратные скобки, поменять в них на , …, а на .

Выпишем условия сопряжения для компоненты :

(2.2.16)

Условие сопряжения для компонент имеют вид, вполне аналогичный (2.2.16).

Рассмотрим граничные условия в перемещениях:

на .