Изложение: Опір матеріалів: інженерні методи розрахунків
σ = Е*ε (7)
Е – модуль Юнга(модуль пружності)
Е = [Па] – фізична константа матеріалу
Підставимо 1 і 4 в 7 і одержимо
∆ l = Nl / EA
EA – жорсткість при розтязі, стиску.
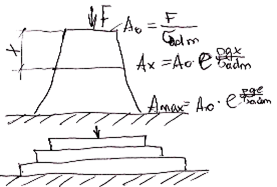
10. Розрахунок на міцність при розтязі, стиску. Врахування власної ваги бруса при розтязі та стиску, брус рівного опору
При великих довжині та густині матеріалу необхідно враховувати вплив власної ваги стрижня на напругу та деформацію. Це стосується таких конструкцій як фундаменти, під будівлі та обладнання, греблі ... Розглянемо стрижень під дією зовн сил і власної ваги. Визначимо нормальну напругу в поперечних перерізах стрижня враховуючи його вагу. За методом перерізів (Q(x) - вага)
N ( x ) = + F + Q ( x ) = F + ρgAx
Визначимо напругу в тому ж перерізі:
σ( x ) = N ( x )/ A = F / A + ρgx
Якщо F = 0, то σ( x ) = ρgx – напруга лише від власної ваги. Аналізуючи цю формулу зауважимо, що напруга залежить від матеріалу, довжини і не залежить выд площі. Подовження від власної ваги визначають за ф-лою:
∆ l = Ql /2 EA
∆ l = Nl / EA – з-н Гука
 |
???? ?????????? ??? ??????? ???? ? ? 2 ???? ?????? ??? ??? ????? ? ?? ????????? ?????????? ????. ??? ??????????? ????????? ??? ???????? ?????? ??????? ???? ????? ?????????? ???? ??????? ?????. ????? ?????, ? ????? ??????? ? ???? ????????? ???????? ? ????? ??????????. ????????? ?????????? ?????? ??????? ???????, ? ???? ????????? ?????????????? ?????????? ???????.
11. Статично невизначені стрижневі сис-ми та метод визначення зусиль у таких сис-мах
Статично невизначеними називають сис-ми, силові фактори в елементах яких тільки з рівнянь рівноваги визначити не можна. У таких сис-мах зв’язків більше ніж потрібно для рівноваги.
Статично невизначена задача визначення силового стану конструкції розв’язують розглядаючи 4 сторони задачі:
1 – статична сторона задачі: складають всі можливі рівняння рівноваги.
2 – геометрична сторона задачі: складають додатково до рівнянь рівноваги, так звані рівняння сумісності деформацій розглядаючи здеформований стан конструкції в цілому.
3 – фізична сторона задачі: на основі закону Гука та закону лінійного теплового розширення виражають зусилля через деформацію, або навпаки.
4 – синтез: розв’язують сумісно статичні, фізичні та геометричні р-ня.
12. Основні властивості статично невизначених сис-м. Початкові та температурні зусилля
Основні в-ті стат невизначених сис-м:
◄ Розподілення зусиль між стрижнями статично невизначеної конструкції залежить від відношення жорсткостей цих стрижнів та від геометрії будови самої конструкції.
◄ Більше зусилля виникає в тому стрижні, що має більшу жорсткість.
◄ Відношення жорсткостей може мати нескінченну к-ть значень, тобто у стат невизначених конструкціях може мати місце нескінченна к-ть варіантів розподілу зусиль.
Із останньої властивості випливає можливість оптимізації розподілу зусиль у стат невизн конструкціях: необхідно знайти таку конструкцію, яка задовольняє умови міцності, жорсткості та стійкостіі є оптимальною за витратами матеріалу, коштів, енергоресурсів, тобто за зведеними витратами.
Початкові зусилля – це зусилля, що виникають до прикладання корисного навантаження. При прикладанні корисних напружень виникає наступний перерозподіл сил: 1-ша група елементів ще більше напружується, але при цьому інша зазнає розвантаження.
При в елементах стат невизн конструкцій виникає так звана температурна напруга. Внаслідок зміни температури стрижня на ∆t непіддатливі опори будуть реагувати на розширення стрижня тобто виникнуть р-ції R1 i R2 . Температурна напруга залежить лише від матеріалу і зміни температури, але не залежить від поперечного перерізу.