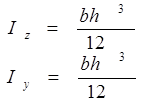Изложение: Опір матеріалів: інженерні методи розрахунків
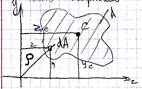
Нехай маємо довільну сис-му координат. За аналогією з моментом сили відносно осі можемо записати вирази:
dSz = y*dA (1)
dSy = z*dA
Sz = ∫ A ydA
Sy = ∫ A zdA (2)
Sz i Sy – статичні моменти плоского перерізу відносно осей координат.
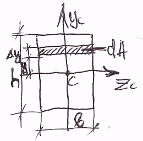
Нехай т С є центром мас попер перер , yc , zc – координати центра мас.
Sz = yc А
Sy = zc А (3)
yc = Sz /А
zc = Sy /А (4)
Враховуючи, що інтеграл за всією площею рівний сумі інтегралів за окремими її складовими, що має n частин:
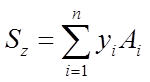 (5)
(5)
простим перерізом вважається такий в якого відомо положення центра мас (Ο, ∆, □, прокатні профілі, кутик, швелер, двотавр). Будь який складений переріз має у своєму складі декілька простих перерізів. Для будь якого складеного перерізу ф-лу 4 можна записати у вигляді
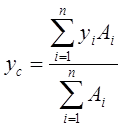
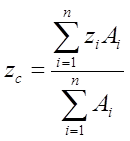 (6)
(6)
14. Моменти інерції плоскої фігури. Моменти інерції простих перерізів
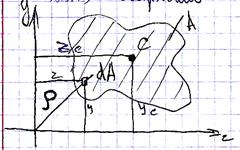 |
?????????????? ??????? ???????? ??????:
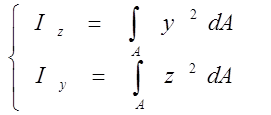 [м4 ]
[м4 ]
- осьові моменти інерції плоского перерізу.
І > 0 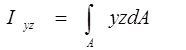 [м4 ]
[м4 ]
- відцентровий момент інерції
Iyz > 0; Iyz < 0; Iyz = 0. Iyz = 0 в тому випадку коли хоча б одна з осей є віссю симетрії перерізу, а також відносно головних осей.
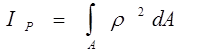
- полярний момент інерції.
Якщо співпадають початки координат у полярній та Декартові сис-мах то ρ2 = z2 +y2
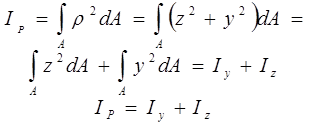
Отже, полярний момент інерції рівний сумі осьових моментів інерції.
а) прямокутний
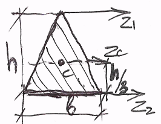 |
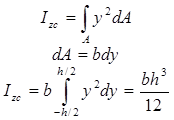
 |