Изложение: Опір матеріалів: інженерні методи розрахунків
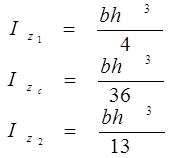
в) круглий
 |
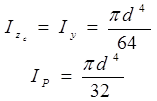
г) кругле кільце
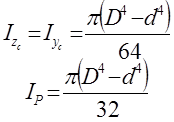
Моменти інерції прокатних профілів див у табл. сортаменту.
 |
15. Залежність між моментами інерції при паралельному перенесенні осей
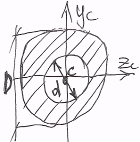
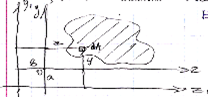
В результаті паралельного зміщення сис-ми координат, координати елементарної площинки dA перетворяться наступним чином

Визначимо моменти інерції відносно осей y1 i z1

Найчастіше розгул задачі про паралельне перенесення центральних осей. В такому випадку SZc = 0;SYc = 0 а ф-ли 1, 2, 3 набувають вигляду

Аналізуючи 4 зауважуємо, що найменше значення моменти інерції мають відносно центральних осей. Віддаляючи паралельно вісь від центральної осі спостерігаємо суттєве збільшення момента інерції на величину а2 А.
 |
16. Залежність між моментами інерції при повороті осей
Повернемо вправо Декартову сис-му координат в додатному напрямі на деякий кут α. В новій сис-мі координат z1 i y1 . Змінились координати:
Z 1 = | OA | + | ED | = zcosα + ysinα (1)
Y 1 = | BD | - | AE | = ycosα – zsinα (2)
1 і 2 – є відомими ф-лами перетворення координат при повороті сис-ми відліку. Визначимо моменти інерції перерізу в новій сис-мі координат.
а) осьові моменти інерції:

б) відцентрові моменти інерції

Таким чином, можна зробити висновок, що при повороті сис-ми координат сума моментів інерції залишається сталою і рівною полярному моменту інерції відносно початку координат. Тобто:
Iy + Iz = Iy 1 + Iz 1 = IP
17. Головні центральні осі та головні моменти інерції
Головними осями інерції називаються такі осі відносно яких моменти інерції набувають екстремальних значень. Головні осі, що проходять через центр мас поперечного перерізу називають головними центральними осями. Визначимо положення головних центральних осей:
Дослідимо ф-лу
![]()
на екстремум, як Iz 1 = f(α)
