Книга: Ряды Фурье Интеграл Фурье Операционное исчисление

При любых вещественных

.

Таким образом, квадратный трехчлен в левой части последнего неравенства сохраняет знак на всей вещественной оси, следовательно, его дискриминант .

Упражнение 1. Доказать свойства скалярного произведения функций 1-3.

Упражнение 2. Показать справедливость следующих утверждений:

а) функция ортогональна функциям и на промежутке при любых целых k и m ;

б) при любых целых k и m функции и ортогональны на промежутке ;

в) функции и , а также и при ортогональны на промежутках и ;

г) функции и не ортогональны на промежутке .

Упражнение 3. Используя свойство нормы 5, доказать неравенство треугольника

.

§ 3. Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье

Счетное множество непрерывных на промежутке функций образуют на этом промежутке ортогональную систему, если

1. , 2. при .

Пусть – ортогональная система функций на промежутке и . По аналогии с (1.2) образуем величины

, (3.1)

где .

Числа называются коэффициентами Фурье функции относительно ортогональной системы .

Ряд

(3.2)

называется рядом Фурье для функции .

В отличие от того, что имеет место в векторной алгебре [см. (1.1)], здесь нельзя утверждать ни того, что суммой ряда Фурье (3.2) является заданная функция , ни даже того, что ряд (3.2) вообще сходится. Тем не менее, частичные суммы ряда (3.2), называемые полиномами Фурье, играют важную роль в задаче аппроксимации функции линейными комбинациями функций .

Термином аппроксимация будем обозначать замену заданной функции другой, близкой к , функцией , более простой или более удобной для исследования. При этом, естественно, возникает вопрос о величине погрешности, связанной с такой заменой. Погрешность аппроксимации обычно оценивается с помощью среднего квадратического отклонения

,

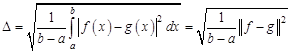или более простой величины

.

Ясно, что чем меньше величина δ, тем ближе располагаются друг к другу графики функций и , тем лучше функция аппроксимирует функцию .

Определим, при каком наборе коэффициентов линейная комбинация