Книга: Ряды Фурье Интеграл Фурье Операционное исчисление

Левая часть последнего равенства, как легко видеть, представляет собой удвоенное среднее значение квадрата функции на промежутке [–L , L ].

Частичные суммы

тригонометрического ряда (5.2) называются тригонометрическими полиномами Фурье. Из формулы (3.3) следует, что средняя квадратическая погрешность, возникающая при замене функции ее тригонометрическим полиномом Фурье,

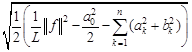. (5.5)

§ 6. Сходимость тригонометрического ряда Фурье. Теорема Дирихле

Функция называется кусочно-монотонной на промежутке , если этот промежуток можно разделить на конечное число частей, на каждой из которых функция монотонна.

Если функция кусочно-непрерывна и кусочно-монотонна на промежутке , то говорят, что на этом промежутке она удовлетворяет условиям Дирихле. Для таких функций справедлива принимаемая нами без доказательства следующая теорема.

Теорема Дирихле. Если функция удовлетворяет условиям Дирихле на промежутке [–L , L ], то ее ряд Фурье (5.2) сходится во всех точках этого промежутка. При этом во внутренних точках промежутка сумма ряда Фурье , если в точке х функция непрерывна; в точках разрыва ; на концах промежутка , где – односторонние пределы в точке а .

Если доопределить (или переопределить) функцию , полагая в точках разрыва и f (–L ) = = на концах промежутка, то в соответствии с теоремой Дирихле

, (6.1)

где коэффициенты по-прежнему определяются формулами (5.3).

Соотношение (6.1) обычно называется разложением функции в тригонометрический ряд Фурье. Члены ряда (6.1)

(6.2)

называются гармониками. Введем в рассмотрение величины и , связанные с коэффициентами Фурье и соотношениями и . Тогда гармоника (6.2) запишется в виде , где – амплитуда гармоники; – ее частота; – начальная фаза. Множество частот образует дискретный частотный спектр функции на промежутке [–L , L ]. Формула (6.1) примет вид

, (6.3)

т.е. функция, удовлетворяющая условиям Дирихле, представляет собой результат сложения бесконечного числа гармоник. При этом амплитуды и начальные фазы слагаемых гармоник зависят от разлагаемой функции, а частотный спектр одинаков для всех функций, заданных на одном и том же промежутке.

Из равенства Парсеваля (5.4) следует

, (6.4)

где .

Таким образом, сумма квадратов амплитуд гармоник равна удвоенному среднему значению квадрата функции на промежутке [–L , L ]. Соотношение (6.4) часто называют энергетическим равенством.

В силу периодичности гармоник из сходимости ряда (6.3) на промежутке [–L , L ] следует его сходимость всюду, т.е. на всей числовой оси. Суммой этого ряда, очевидно, будет 2L- периодическая функция , которая на промежутке [–L , L ] совпадает с заданной функцией . Функция , определенная указанным образом, называется периодическим продолжением.

Теорема Дирихле (другая формулировка). Если функция удовлетворяет условиям Дирихле на промежутке [–L , L ], то тригонометрический ряд Фурье (6.1) сходится всюду к ее периодическому продолжению.

Замечание . Если функция , заданная для всех , является 2L- периодической, то ее периодическое продолжение совпадает с самой функцией, и, следовательно, ряд Фурье (6.1) представляет функцию на всей числовой оси. В этом случае можно

получить другие, иногда более удобные по сравнению с (5.3), формулы для коэффициентов Фурье:

, (6.5)

где с – любое число.

Вместо того, чтобы устанавливать справедливость формул (6.5), докажем более общее утверждение: если функция имеет период Т , то интеграл не зависит от а . Действительно,