Книга: Ряды Фурье Интеграл Фурье Операционное исчисление

. (9.1)

2. Обобщенная теорема Пифагора. Если , то

.

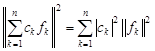Доказать свойства 1 и 2 следует самостоятельно.

3. Неравенство Коши – Буняковского. Если функции и непрерывны, то .

В самом деле, если , то на , и доказываемое неравенство выполняется. Пусть . Число очевидно, не отрицательно. С другой стороны, по формуле (9.1), где и , имеем

.

Таким образом, , а так как , то , что и требовалось доказать.

Пусть теперь система комплексных функций

(9.2)

ортогональна на промежутке . Сопоставим функции ее ряд Фурье

(9.3)

где коэффициенты Фурье

.

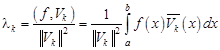Введем обозначения: – частичная сумма ряда Фурье; – произвольная линейная комбинация функций где .

Тогда, так же, как для вещественных функций (см. § 3), выполняется неравенство

(9.4)

где , причем равенство имеет место тогда и только тогда, когда , т.е. среди всех функций функция дает наилучшее среднеквадратическое приближение к функции