Контрольная работа: Динамическое поведение механической системы с упругими связями

Теперь вычислим правую часть уравнения (1) – сумму мощностей внешних и внутренних сил, при этом учтем, что мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность пары сил – скалярному произведению вектора пары на угловую скорость твердого тела, к которому приложена пара:

Или

Рассматриваемая нами механическая система является неизменяемой, так как входящие в систему тела абсолютно твердые, а нити — абсолютно гибкие и нерастяжимые. Следовательно, скорости их точек относительно друг друга равны нулю и сумма мощностей внутренних сил также будет равна нулю

(6)

С учетом кинематических соотношений (3) сумму мощностей внешних

сил преобразуем к виду:

(7)

Где

- приведенная сила.

Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины равно сумме статического и динамического удлинений

Тогда

Приведенная сила в развернутом виде примет вид:

(8)

Где - приведенная жесткость,

- приведенный коэффициент сопротивления.

Подставляя выражения (4), (6) и (7) в (1), получаем после сокращения на дифференциальное уравнение движения системы:

(9)

Учтем, что при равновесии системы (возмущающая сила отсутствует) скорость и ускорение груза равны нулю по определению , а координата груза равна нулю в силу постановки задачи (начало отсчета совпадает с положением равновесия груза 1 S=0). В этом случае уравнение (9) приводится к виду , и условием равновесия системы будет служить уравнение

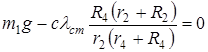
Откуда

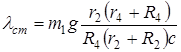(10)

Подставляя (10) в уравнение (9) и учитывая формулу (8) для приведенной силы, получаем дифференциальное уравнение движения системы

Представим данное уравнение в виде:

(11)

где введены коэффициенты, имеющие определенный физический смысл: