Контрольная работа: Динамическое поведение механической системы с упругими связями

Иными словами, необходимо удовлетворить следующим условиям:

1) нити должны быть натянутыми при движении системы;

2) величина силы сцепления должна обеспечивать движение катка без проскальзывания;

3) перемещение центра масс катка не должно превышать величины предельного значения удлинения пружины.

Данные условия представим в математическом виде

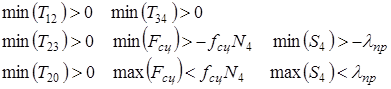(25)

Для определения значений внутренних параметров механической системы - масс тел и коэффициента жесткости пружины c, - обеспечивающих ее функционирование в соответствие с предложенной математической моделью, выберем в качестве анализируемых величин

1) реакции сил натяжения нитей;

2) силу сцепления катка с опорной плоскостью;

3) перемещения центра масс катка 4;

Исследуем изменение этих функций, в зависимости от масс тел входящих в механическую систему, а также жесткости упругого элемента.

Ограничимся состоянием установившегося движения. В этом случае закон движения груза, его скорость и ускорение имеют вид

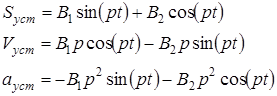
Функции сил натяжений нитей и сцепления катка представим в виде:

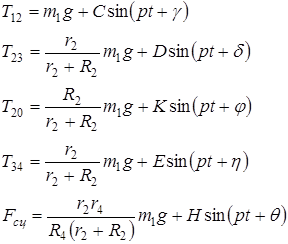(26)

где коэффициенты, входящие в (26) равны:

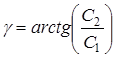
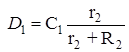
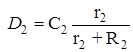
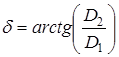
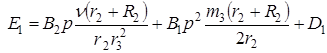
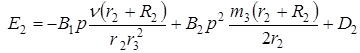
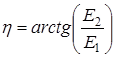
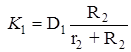
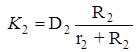
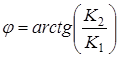
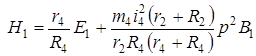
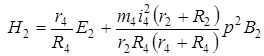
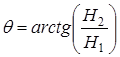
Условия (25), обеспечивающие адекватность движения системы математической модели (11), (12) можно теперь представить в виде

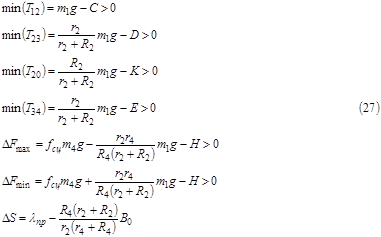
Так как все коэффициенты, входящие в соотношения (27) являются

функциями внутренних параметров механической системы и с, то

вычисление зависимостей представим в виде процедуры S(M1,M3,M4,W) пакета Mathcad. Выражение для функции ΔS(M1,M3,M4,W), в силу несложности ее преобразования, получим позже.

В дальнейшем, ограничимся исследованием влияния масс и . Установим интервалы их изменения. Для этого рассмотрим механическую систему в состоянии резонанса. Если , то