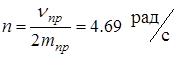- показатель степени затухания колебаний.

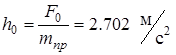- относительная амплитуда возмущающей силы.

Начальные условия:

(12)

Уравнения (11), (12) представляют математическую модель для решения второй задачи динамики.

2. Определение реакций внешних и внутренних связей

Для решения этой задачи расчленим механизм на отдельные части и построим расчетные схемы для каждого тела (рис.3). На расчетных схемах, помимо ранее введенных сил, показаны реакции (силы натяжения) нитей, связывающих груз и блок 2, блок 2 и горизонтальную поверхность, блоки 2 и 3, блок 3 и каток 4: .

К каждому телу, изображенному на расчетной схеме (рис. 3), применим

две основные теоремы механики материальной системы:

теорему об изменении количества движения

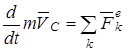(13)

и теорему об изменении кинетического момента относительно оси z, проходящей через центр масс твердого тела

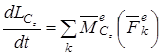(14)

Для каждого тела данные уравнения запишем в проекциях на оси координат соответственно схемам рис. 3:

тело 1 :

тело 2 :

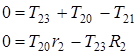
тело 3 :

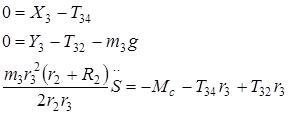
тело 4 :

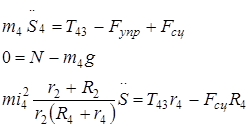
Из этих уравнений можно получить формулы для реакций связей:

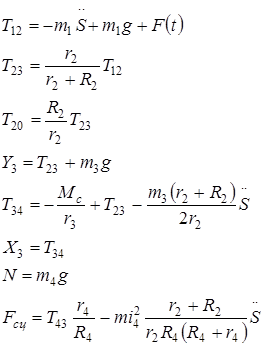(15)

Для проверки выражений реакций связей, подставим их в оставшееся неиспользованное уравнение:

После подстановки и упрощений получаем уравнение, совпадающее с уравнением (11).

3. Определение закона движения системы

Найдем решение дифференциального уравнения движения механической системы (11). Данное дифференциальное уравнение относится к классу линейных неоднородных дифференциальных уравнений с постоянными коэффициентами. Решение таких уравнений можно найти аналитически. Общее решение неоднородного дифференциального уравнения (11) складывается из общего решения однородного уравнения

(16)

соответствующего данному неоднородному уравнению, и какого-либо частного решения уравнения (11), т.е.