Контрольная работа: Динамическое поведение механической системы с упругими связями

Решение однородного уравнения (16) ищем в виде функции

(18)

Подставив (18) в (16), получим:

Так как мы ищем нетривиальное решение, то . Следовательно, должно выполняться условие

Данное уравнение называется характеристическим уравнением дифференциального уравнения (16). Это уравнение имеет два корня:

Вид общего решения уравнения (16) зависит от типа корней его характеристического уравнения. Возможны следующие случаи:

1) n<k – корни характеристического уравнения комплексные сопряженные:

и общее решение однородного уравнения имеет вид

(19)

Здесь - постоянные интегрирования.

2) n>k – корни характеристического уравнения действительные и различные

и общее решение однородного уравнения имеет вид

3) n=k - корни характеристического уравнения кратные: и общее решение однородного уравнения имеет вид

В рассматриваемом случае , . Поскольку n<k, то общее решение однородного уравнения (16) имеет вид:

или (20)

Здесь , а коэффициенты связаны между собой соотношениями:

Определим частное решение неоднородного дифференциального уравнения (11). Данное решение ищем в виде правой части

(21)

где коэффициенты связаны между собой соотношениями

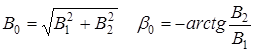
Подставляя (21) в уравнение (11), после несложных преобразований получим