Множество называется моментным пространством класса F относительно системы функций .

Лемма 1. Пусть системы u₁ (t), …, u_n (t) и u₁ (t), …, u_n (t), u_{n +1} (t) образуют T₊ -системы на [0, ¥) такие, что . Тогда отношение невозможно для и, если , то

.

Доказательство. Допустим, что , где k£n, и A₁ , …, A_k – множества строгого знакопостоянства функции D=g - f. Для векторов рассмотрим матрицу

.

Так как

, ,

то есть

, (1)

где d_i (-1)^{k - i} , и d_i =0, для всех векторов .

Из (1) следует, что detH()=0 для любых . С другой стороны, применив k раз теорему о среднем к H(), получим

, (2)

где 0£x₁ <x₂ <…<x_k <¥. Так как векторы линейно зависимы, то их можно дополнить до системы линейно независимых векторов . Из (2) получаем .

Пусть теперь и .

Так как

, (3)

где d_i =(-1)^{n +1- i} , , то

,

где H – матрица, записанная в (3) слева, - матрица, получаемая из H удалением (n+1)-ых строки и столбца. Применив теорему о среднем, получаем detH>0, . Вместе с равенством d_{n +1} =1 это означает, что d>0.

Определение 3. Скажем, что последовательность {f_i }_{i ³ 1} функций на [0, ¥) относительно класса U слабо сходится к функции f, если

для всех uÎU.

Определение 4. Множество AÌF_U назовем (k, U) окрестностью функции f в F, если fÎA и множество А имеет вид , где V открыто, при , при .

Множество AÌF_U назовем (k, U)-открытым, если каждая функция fÎA имеет (k, U) окрестность, состоящую из функций множества А.

Определение 5. Класс F непрерывных слева, неотрицательных функций на [0, ¥) назовем нижним U-индексационным с дефектом n, если:

1. Класс F равномерно ограничен, то есть существует L>0, такое, что f(t)£L при t³0, fÎF;

2. ;

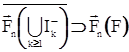3. Множества I_k ^- (k-1, U) – открыты для всех k>n+1;

4. Из любой последовательности {f_i }_{i ³ 1} ÌI^- _{k +1} (k>n) такой, что

,