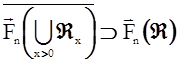(2)

Лемма 1. .

Доказательство. Пусть . Из выпуклости множества следует, что точка является внутренней точкой некоторого (n+1)-мерного симплекса, лежащего в , т. е. существуют векторы , и числа l₁ >0, …, l_n >0, l_{n +1} >0 такие, что .

Из (2) следует существование последовательностей , таких, что

.

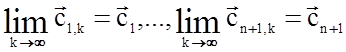Тогда для достаточно больших k выполнено равенство

,

где , .

Следовательно, .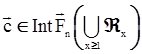

Из леммы 1 следует, что для достаточно больших x. Так как класс Â_x является индексационным на [0, x], то ([5])

,

,

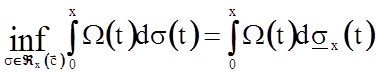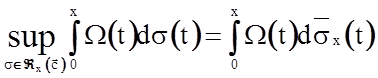где , () – ФР с нижним (верхним) индексом n+1 в классе Â_x .

Так как ФР 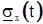имеет индекс (n+1)^- в Â и 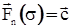, то

.

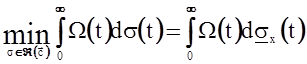Из (1) следует, что

.

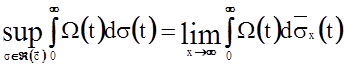Вид экстремальных ФР и для рассматриваемых классов имеется в [5].

2⁰ . Второй подход продемонстрируем на примере класса Â₀ всех ФР на [0,¥).

Лемма 2. Если u₀ , u₁ , …, u_n – T₊ -система на [0,¥), то для всех i и j существуют пределы .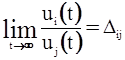

Доказательство. Из определения T₊ -системы следует, что для произвольных i, j и чисел a,b функции u_j (t) и au_j (t)+bu_j (t) обращаются в нуль более, чем в n+1 точках.

Пусть х – наибольшее решение уравнения u_j (t)=0. Рассмотрим уравнение

au_j (t)+bu_j (t)=0, t>x. (3)

Уравнение 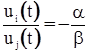(u_i (t)¹0, t>x) имеет не более (n+1) решений на (x, ¥) при любых a,b.

Пусть , .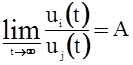

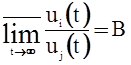Допустим, что 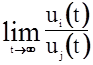не существует, т. е. А<B.

Введем последовательности {t_i }_{i ³ 1} , {t_i }_{i ³ 1} , удовлетворяющие условиям:

а) t_k ®¥,t_k ®¥ при k®¥;

б) , ;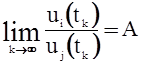

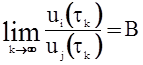в) t₁ <t₁ <t₂ <t₂ <…<t_m <t_m <… .