Контрольная работа: Экстремальная задача на индексационных классах
Пусть Â – некоторый класс функций распределения (ФР) на [a, b], -¥<a<b<¥; W(t) – (n+1) раз непрерывно дифференцируемая функция на [a, b], причем W( k ) (t)>0 для tÎ[a, b] и ![]() ; c1 , …, cn – вещественные константы; xÎ[a, b].
; c1 , …, cn – вещественные константы; xÎ[a, b].
Экстремальная задача. Найти супремум и инфимум интеграла

на множестве ![]()
![]() ФР из Â, удовлетворяющих ограничениям
ФР из Â, удовлетворяющих ограничениям
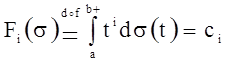 ,
, ![]() .
.
Для классов Âo - всех ФР на [a, b] и ВL – ФР на [a, b], удовлетворяющих условию 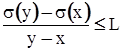 , -¥<x<y<¥, задача решена в [1].
, -¥<x<y<¥, задача решена в [1].
Важность решение экстремальных задач на разных классах ФР обоснована, например, в [1 - 5].
Задача при x=b решена в [4] для мажоризационных классов.
Анализ задачи на мажоризационных классах в общем случае наталкивается на трудности. Выход мы видим в рассмотрении классов с иной структурой – индексационных классов ФР.
Ниже предполагается, что Â - индексационный с дефектом n класс ФР на [a, b]. Определение индексационного с дефектом n класса приведено в [5]. Индексационными являются многие важные классы ФР, например, Âo , BL , класс унимодальных ФР на [a, b] и др.
Обозначим (k³1,AÌÂ, sÎÂ): Ik + (Ik - ) –множество всех ФР из Â, имеющих индекс k+ (k- ); ![]() ;
; ![]() - пространство моментов порядка k;
- пространство моментов порядка k; 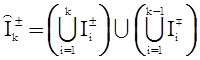 ;
; ![]() ;
; ![]() ,
, ![]() .
.
Основной результат работы содержится в утверждении.
Теорема. Пусть ![]() ,
, ![]() . Тогда:
. Тогда:
1. 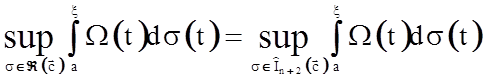 ,
,
2. 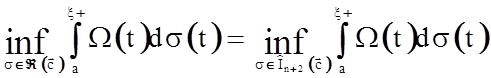
![]() ,
,
3. 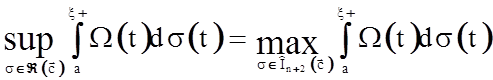 ,
,
4. 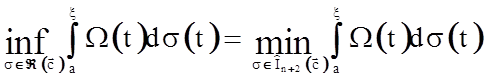 .
.
§ 2 Свойства отображения 
Нам понадобятся два факта из [6].
1. Для любого ![]() существует и единственная ФР
существует и единственная ФР ![]() .
.
2. Если ![]() , то множество
, то множество ![]() одноэлементно. Если
одноэлементно. Если ![]() , то существуют непрерывные, однопараметрические семейства
, то существуют непрерывные, однопараметрические семейства ![]() (т. е.
(т. е. ![]() при
при ![]() и
и ![]() (значок Þ обозначает слабую сходимость)) и
(значок Þ обозначает слабую сходимость)) и ![]() ФР такие, что
ФР такие, что ![]() ,
,![]() ,
, ![]() , для aÎ(0,1) и
, для aÎ(0,1) и ![]() для bÎ(0,1).
для bÎ(0,1).
Пусть ![]() и
и 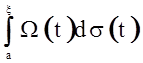 , где
, где ![]() , xÎ[a, b].
, xÎ[a, b].
Функция Ás непрерывна слева на [a, b] и Ás (a)=0 для всех sÎÂ. Так как W(t)>0 при tÎ[a, b], то Ás (x) не убывает по x.
Далее, из sk Þs при k®¥ следует ![]() Á
Á![]() ÞÁs . Следовательно, семейства распределений {Á
ÞÁs . Следовательно, семейства распределений {Á![]() } и {Á
} и {Á![]() } непрерывны.
} непрерывны.
Определение 1. Функция f имеет на [a, b] m строгих перемен знака, если существуют множества B0 (f)<…<Bm (f) (под X<Y (X, YÌR1 ) понимаем x<y для всех xÎX, yÎY) из [a, b] такие, что (-1)j f(x)>0 (или (-1)j +1 f(x)>0 при xÎBj (f), ![]() и f(x)=0 при
и f(x)=0 при 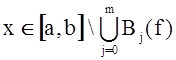 .
.
Лемма 1. Для любого распределения Á![]() (Á
(Á![]() ) и для любого Ám ,
) и для любого Ám , ![]() , функция Ám - Á
, функция Ám - Á![]() (Ám - Á
(Ám - Á![]() ) имеет либо n+1, либо n+2 строгих перемен знака на [a, b].
) имеет либо n+1, либо n+2 строгих перемен знака на [a, b].
Доказательство. Предположим, что функция Ám - Á![]() имеет более n+2 строгих перемен знака. Тогда существуют a<x0 <x1 <…<xn +3 £b такие, что (-1)i [Ám
имеет более n+2 строгих перемен знака. Тогда существуют a<x0 <x1 <…<xn +3 £b такие, что (-1)i [Ám ![]() -Á
-Á![]() ] > 0,
] > 0, ![]() . Кроме того, Ám (a)=Á
. Кроме того, Ám (a)=Á![]() (a)=0. Следовательно, существуют точки y0 Î[a, x0 ), y1 Î[x0 , x1 ), …, yn +3 Î[xn +2 , xn +3 ) такие, что функция (-1)i [m(t) - ha (t)] возрастает в точке yi ,
(a)=0. Следовательно, существуют точки y0 Î[a, x0 ), y1 Î[x0 , x1 ), …, yn +3 Î[xn +2 , xn +3 ) такие, что функция (-1)i [m(t) - ha (t)] возрастает в точке yi , ![]() , что противоречит условию
, что противоречит условию ![]() .
.
Равенство ![]() запишем в виде
запишем в виде
 Ás (t)=ci ,
Ás (t)=ci , ![]() ,
,
где  ,
, ![]() , с0 = 1.
, с0 = 1.