Контрольная работа: Электромагнитные волны

Таким образом, все векторы, характеризующие электромагнитное поле ( и ), выражаются через две вспомогательные функции:. Следовательно, теперь задача состоит в том, чтобы определить эти две функции. Для этого подставим (4.3[4]) и (4.6[4]) в первое уравнение Максвелла.

,

.

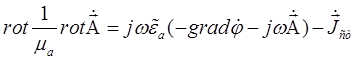Учитывая известное из высшей математики тождество , где - любая векторная величина, преобразуем полученное выражение следующим образом:

.

.

Поскольку - произвольные вспомогательные функции, то зададим их таким образом, чтобы выполнялось условие:

. (4.8[4])

Условие (4.8[4]) получило название условие калибровки Лоренца.

С учетом (4.8[4]) окончательно получаем:

, (4.9[4])

где: – называют волновым числом,

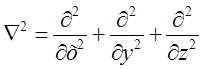– оператор Лапласа.

Аналогичным образом, подставляя в третье уравнение Максвелла уравнение (4.7[4]), затем, учитывая условие калибровки Лоренца и известное тождество , где – некая скалярная величина, после несложных преобразований получим:

. (4.10[4])

Таким образом, мы получили два неоднородных дифференциальных уравнения второго порядка для функций . Среди множества решений выбирается то, которое удовлетворяет условию калибровки (4.8[4]), и затем уже с помощью (4.2, 4.3, 4.6, 4.7 [4]) определяются векторы электромагнитного поля.

Опуская ввиду громоздкости строгий вывод решения неоднородных дифференциальных уравнений (4.9[4]) и (4.10[4]), приведем лишь конечный результат решения этих уравнений:

, (4.11[4])

, (4.12[4])

где: V – область пространства, содержащая сторонние источники;

r – расстояние от источника до точки наблюдения (см. рис.1).

Рис.1. К пояснению выражений для электродинамических потенциалов

Рассмотрим простейший излучатель электромагнитных волн в виде короткого отрезка провода. Дадим определение:

Элементарным электрическим излучателем (ток I_ст вибратором) называют отрезок провода, вдоль которого течет переменный ток с постоянной амплитудой I_{ст m} = const, причем длина l этого проводника значительно меньше излучаемой длины волны l.

Представим ток I_ст в комплексной форме:

.

Применим к отрезку провода, по которому протекает ток I_ст , закон сохранения заряда (см. ур. 1.26[4])

,