Контрольная работа: Электромагнитные волны

4. Вернемся к фазе составляющих электромагнитного поля излучателя (wt – kr) = w(t – r/v). Заметим, что она зависит как от времени t, так и от расстояния r. Из курса общей физики известно, что любой процесс, описываемый уравнением вида: А = А_m cos(х), есть волновой процесс. Следовательно, исходя из (4.19[4]), заключаем, что электромагнитное поле в дальней зоне представляет собой электромагнитную волну, изменяющуюся во времени и в пространстве. Причем векторы и лежат перпендикулярно к направлению распространения r (т.к. у них индексы q и j) находятся в фазе и взаимно перпендикулярны друг к другу.

К основным параметрам элементарного электрического излучателя обычно относят:

- диаграмму направленности;

- мощность и сопротивление излучения.

На практике, как правило, основной интерес представляет дальняя зона излучения, поэтому данные параметры будут рассматриваться лишь применительно к этой зоне.

Диаграммой направленности называют зависимость нормированной амплитуды напряженности поля излучателя в дальней зоне от направления (т.е. от угловых сферических координат q и j) при постоянном расстоянии от излучателя (т.е. при r = const):

,

где: Е_mmax ,Н_mmax – максимальное амплитудное значение Е_m (q,j) и Н_m (q,j), соответственно.

Из (4.19[4]) имеем, что максимальное значение, например Е_m (q,j), при изменении q и j соответствует:

.

Следовательно, диаграмма направленности элементарного электрического излучателя:

, (4.21[4])

и не зависит от угла j. Максимум излучения лежит в экваториальной плоскости вибратора (q=90⁰ ); вдоль его оси излучения нет. В сферической системе координат диаграмма направленности представляет собой пространственную фигуру в виде тора (см. рис.6).

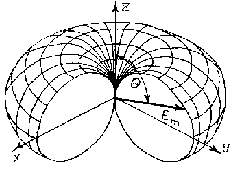
Рис. 7. Диаграмма направленности элементарного электрического излучателя

Определим теперь среднее значение вектора Пойнтинга элементарного элек-трического вибратора в предположении, что по излучателю длиной l протекает переменный ток I с частотой w. Для переменных (т.е. гармонических) полей П_ср определяется выражением (3.18[4]):

.

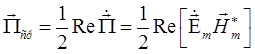Для дальней зоны из (4.18[4]) получаем:

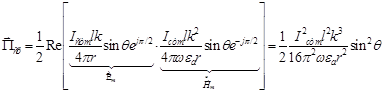. (4.22[4])

Для того, чтобы определить мощность, излучаемую вибратором, мысленно окружим излучатель поверхностью S. Напомним, что вектор Пойнтинга характеризует плотность потока мощности, проходящей через единичную поверхность. Следовательно, проинтегрировав по всей поверхности S, мы определим мощность излучения излучателя:

.

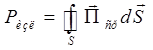Поверхность S удобно взять в виде сферы, тогда, учитывая, что элементарная площадка dS выражается через угловые сферические координаты dq и dj как dS = r² sinqdqdj и расположена по нормали к вектору , получим:

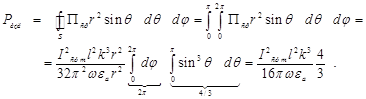(4.23[4])

Согласно полученному выражению мощность излучения пропорциональна квадрату амплитуды переменного тока, протекающего по излучателю. В этом смысле имеется прямая аналогия между выражением (4.23[4]) и обычным выражением для мощности переменного тока, выделяемой на некотором активном сопротивлении: 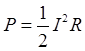. Поэтому (4.23[4]) можно представить в следующем виде:

,

где: 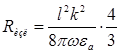- называют сопротивлением излучения. (4.24[4])

Сопротивление излучения имеет очень важное значение в теории антенн, поскольку, как несложно заметить из (4.24[4]), оно характеризует излучательную способность антенной системы.

Преобразуем выражение для R_изл учитывая, что :

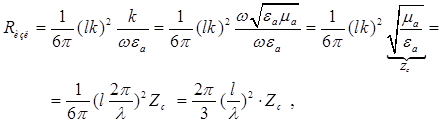(4.25[4])