Контрольная работа: Электромагнитные волны

Подставив числовые значения в (6.7 [1]), получим:

2. Определим длину волны в среде.

Так как , то потери происходят как в проводящих средах, соответветственно длина волны определяется по формуле:

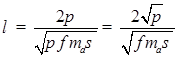; (6.28[1])

Подставив числовые значения в (6.28[1]), получим:

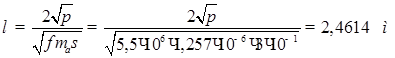
3. Определим расстояние, на котором длина волны убывает на 100 дБ.

Рис.10Уменьшение амплитуды плоской волны при распространениии в среде с потерями.

Расстояние Z, на котором амплитуда волны убывает (затухает) на 100 дБ, найдем, используя закон изменения амплитуды вдоль оси распространения, который можно записать как:

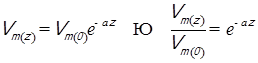; (3.8[2]), где

коэффициент ослабления плоской волны в среде, равный:

; (6.8 [1])

Подставив числовые значения в (6.8 [1]), получим:

Так как амплитуда затухает на 100 дБ, то отношение 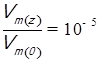, тогда:

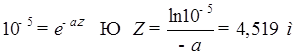
4. Определимотношение модуля плотности тока проводимости к модулю плотности тока смещения.

По условию задачи , соответветственно здесь плоская электромагнитная волна распространяется как в реальной среде, а в реальных средах, в отличии от свободного пространства потери волны возникают по двум причинам. Во-первых, потери связаны с конечной проводимостью среды (потери на джоулевое тепло), во вторых, потери возникают из-за явления поляризации диэлектрика, которое в конечном счете также приводит к тепловым потерям. Характер потерь можно оценить вычислив отношение модуля плотностей тока проводимости и тока смещения:

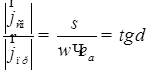; (1.78 [1])

Это отношение называется тангенсом угла потерь. В нашем случае, согласно вычислений по (2.12 [2]), .

Задача 2

Цилиндрический резонатор имеет диаметр D = 0,06 м, длину 0,05 м, заполнен полиэтиленом (относительная проницаемость = 2,5). Определить: 1.Резонансную частоту колебания E.

2.Резонансную частоту колебания H.

3.Добротность колебания E при значении поверхностного сопротивления RОм/м.

4.Полосу пропускания резонатора на колебании E.

Рис.10Цилиндрический резонатор

Дано: D=0,06м; =2,5; l=0,05м;