Контрольная работа: Корреляционный анализ

При построении корреляционных моделей исходят из выполнения условий случайности результатов наблюдений и нормальности закона распределения анализируемой h -мерной генеральной совокупности, что обеспечивает линейный характер изучаемой зависимости между наблюдаемыми признаками и позволяет использовать в качестве показателей силы стохастической (вероятностной) связи парные, частные и множественные коэффициенты корреляции и детерминации.

Понятие "корреляционная зависимость"

В статистических исследованиях выделяют два вида связи между случайными величинами: функциональную и стохастическую.

Зависимость признаков называется функциональной, если каждое наблюдаемое значение зависимой переменной однозначно определяется по полученным в том же самом наблюдении значениям остальных переменных согласно некоторому правилу: , единому для всех наблюдений.

Стохастической зависимостью переменной от переменных называется такое отношение между случайными величинами , при котором каждой реализации случайного вектора однозначно соответствует некоторое условное распределение вероятностей случайной величины , при этом, по крайней мере, двум возможным различным реализациям отвечают неодинаковые распределения.

В отличие от функциональной зависимости, когда каждому набору значений объясняющих переменных соответствует только одно значение объясняемой переменной , при стохастической зависимости любой допустимой совокупности значений отвечает множество возможных значений зависимой переменной .

Корреляционной зависимостью переменной от переменных называется функциональная зависимость условного математическим ожидания случайной величины от реализации случайного вектора .

Корреляционная зависимость является лишь одной из частных форм стохастической связи между случайными величинами и не исчерпывает в общем случае весь объем понятия "стохастическая зависимость".

Функция , устанавливающая зависимость условного математического ожидания от возможных значений случайных величин , называется функцией регрессии случайной величины на случайный вектор .

Если функция регрессии представима как линейная комбинации своих аргументов:

,

где - некоторые константы, то соответствующая корреляционная зависимость называется линейной.

Аналитическое задание корреляционной зависимости в виде

называется уравнением регрессии случайной величины на случайный вектор .

Двумерная корреляционная модель

Анализируется корреляционная зависимость между двумя признаками , .

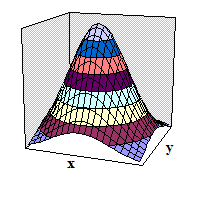
Предполагается, что распределение вероятностей двумерной случайной величины подчинено закону Гаусса, т.е. плотность совместного распределения , определяется формулой:

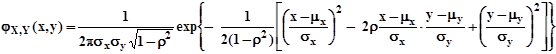
содержащей пять параметров:

- математическое ожидание ;

- математическое ожидание ;

- дисперсия ;

- дисперсия ;

- коэффициент корреляции между , .

Коэффициент корреляции как мера тесноты стохастической связи между двумя случайными величинами

Из условия нормальности совместного распределения признаков , непосредственно вытекает, что распределение каждого их них также подчинено закону Гаусса с соответствующими параметрами:

;

.

Если , то из выражений, задающих двумерную и одномерные плотности распределения вероятностей , , следует, что , т.е. , есть независимые между собой случайные величины.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--