Контрольная работа: Корреляционный анализ

имеет распределение Стьюдента с числом степеней свободы, равным .

При уровне значимости гипотеза отвергается, если выполняется неравенство , в котором под символом понимается критическое значение, удовлетворяющее уравнению

.

При отвержении основной гипотезы заключают, что признаки , связаны линейным корреляционным соотношением, в ином случае делают вывод, что на основе имеющейся выборки корреляционная зависимость между ними не установлена.

Если в результате проверки гипотеза будет отвергнута, то полагают, что коэффициент корреляции значимо (существенно) отличается от нуля, а рассчитанное по статистическим данным значение r может быть использовано в качестве его точечной оценки.

Интервальная оценка коэффициента корреляции

корреляционная регрессия уравнение математический

При построении доверительного интервала для неизвестного коэффициента корреляции используется специальная функция - -преобразование Фишера (гиперболический арктангенс) выборочного коэффициента корреляции r :

.

- возрастающая нечетная функция: z (- r ) = - z ( r ) .

Распределение вероятностей значений приближается (тем более точно, чем больше объем выборки n ) нормальным распределением вероятностей с параметрами:

и .

Статистика имеет асимптотическое стандартное нормальное распределение .

Асимптотически точный доверительный интервал надежности для нормированного отклонения z :

,

где - квантиль уровня распределения , т.е. корень уравнения .

Доверительный интервал для математического ожидания :

.

Величиной в выражении можно пренебречь, принимая во внимание, что она при есть бесконечно малая более высокого порядка в сравнении с .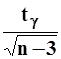

Доверительный интервал для гиперболического арктангенса коэффициента корреляции :

.

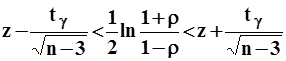Решение относительно данного двойного неравенства приводит к искомому доверительному интервалу для коэффициента корреляции:

,

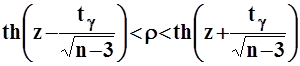с границами, определяемыми как значения гиперболического тангенса 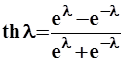для значений , равных соответственно 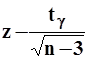и .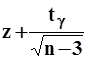

Функция задает преобразование, обратное -преобразованию Фишера. Следовательно, .

Этапы определения ДИ для коэффициента корреляции

- находится выборочный коэффициент корреляции r ;

- выполняется прямое преобразование Фишера значения r : ;

- выбирается квантиль , исходя из условия ;

- вычисляются значения 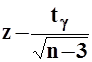и 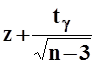;