Контрольная работа: Корреляционный анализ

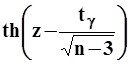и .

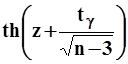Доверительные интервалы для коэффициентов регрессии

Их построение осуществляется в соответствии с общей схемой. При этом используются статистики:

; ,

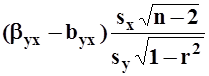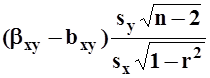имеющие распределение Стьюдента с числом степеней свободы, равном .

;

,

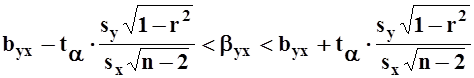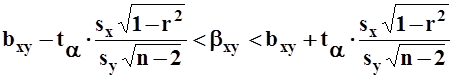где - корень уравнения .

Многомерная корреляционная модель

Предполагается, что совместное распределение анализируемых случайных переменных (признаков) подчинено h -мерному нормальному закону.

Типовые задачи

¨ определение тесноты связи между некоторыми переменными при фиксировании или исключении влияния остальных переменных;

¨ определение тесноты связи одной из рассматриваемых переменных с совокупностью всех остальных переменных, включенных в анализ.

Корреляционная матрица

Начальный этап многомерного корреляционного анализа количественных признаков состоит в оценке (приближении) на основе выборочных данных матрицы

,

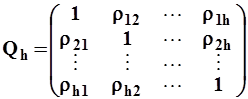элементы которой 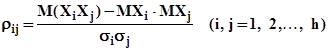- парные коэффициенты корреляции переменных .

Выборочная корреляционная матрица

В качестве статистического аналога корреляционной матрицы принимается матрица

,

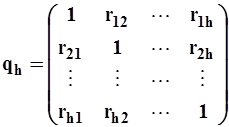здесь 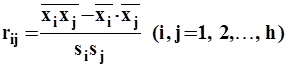- выборочные парные коэффициенты корреляции переменных .

Свойство корреляционных матриц

Матрицы , q_h симметричны относительно главной диагонали.

Вся имеющаяся для анализа статистическая информация о зависимостях между случайными величинами содержится в выборочной корреляционной матрице .

Однако раскрытие многообразия взаимосвязей данных переменных непосредственно по их парным коэффициентам корреляции невозможно. Для проведения исследования при решении указанных типовых задач необходимо вычислять также частные и множественные коэффициенты корреляции, представляющие собой определенные действительные функции матрицы .

Частный коэффициент корреляции

,

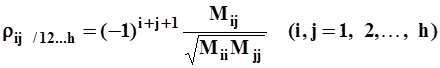где - минор элемента матрицы , т.е. определитель матрицы, получающейся из корреляционной матрицы удалением -ой строки и -го столбца.

Свойства частного коэффициента корреляции

обладает всеми свойствами парного коэффициента корреляции , т.к. является коэффициентом корреляции для их условного двумерного распределения. В отличие от парного коэффициента корреляции , на величине которого сказывается не только влияние переменных друг на друга, но и воздействие остальных переменных, частный коэффициент корреляции позволяет характеризовать тесноту связи между признаками в «чистом» виде, исключая при анализе зависимости влияние других переменных. Если парный коэффициент корреляции больше соответствующего частного коэффициента , то можно заключить, что остальные рассматриваемые переменные усиливают взаимосвязь между изучаемыми величинами . Уменьшение значения парного коэффициента корреляции, в сравнении с отвечающим ему частным коэффициентом корреляции, свидетельствует об ослаблении связи между исследуемыми величинами в результате воздействия других переменных.

Выборочный частный коэффициент корреляции

Точечная оценка определяется по формуле:

,