Контрольная работа: Корреляционный анализ

I. При фиксировании значения одной случайной величины в системе случайных величин трехмерное нормальное распределение данных величин становится условным двумерным нормальным распределением, определяемым пятью параметрами.

Если фиксировано, например, значение случайной величины , то условное двумерное нормальное распределение характеризуется следующими параметрами:

; ;

; ;

.

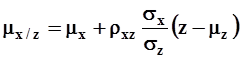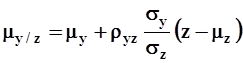Линейная корреляционная зависимость между величинами при фиксированном значении случайной величины графически выражается прямыми регрессии в плоскости :

;

.

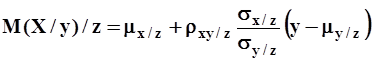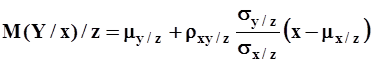II. При фиксированных значениях двух переменных в системе случайных величин трехмерное нормальное распределение есть определяемое двумя параметрами условное одномерное нормальное распределение соответствующей переменной.

В частности, при фиксированных значениях компонент двумерного случайного вектора совместное распределение переменных становится условным одномерным нормальным распределением случайной величины , параметрами которого являются условное математическое ожидание

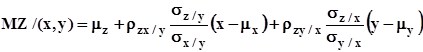
и условная дисперсия , совпадающая с - остаточной дисперсией относительно плоскости регрессии на :

.

Уравнение регрессии на может быть представлено в виде:

,

где 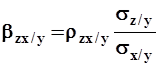; 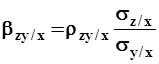- частные коэффициенты регрессии.

Для расчета условн