Контрольная работа: Кручение упругопластического стержня

5. на ;

6. на ;

7. на ;

Из второго условия следует, что уравнение равновесия запишется в виде:

(1.1)

Тогда допустимые поля напряжений принадлежат множеству

(1.2)

Последние два условия задают поворот точек верхнего сечения вокруг оси , где – угол закрутки на единицу длины.

В соответствии с принципом Хаара-Кармана поле минимизирует функционал

(1.3)

Можно показать, что решение этой задачи таково, что все компоненты , кроме и , равны нулю. Тогда из уравнений равновесия остается только одно:

(1.4)

Введем функцию тока и положим:

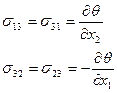
Тогда уравнение (1.4) автоматически выполнено.

Уравнения на части границы можно представить в виде:

(1.5)

С другой стороны, (1.6)

Следовательно, , т.е. на границе . Не умаляя общности, можем положить на . Значит, .

Рассмотрим условие пластичности Мизеса:

, – предел текучести материала. (1.7)

В данном примере, . Отсюда, почти везде на . Переформулировав условие Мизеса в терминах , получаем

(1.8)

В итоге принцип Хаара-Кармана приводит к следующей вариационной задаче:

З1 : Найти такое, что достигает минимума функционал

,

где , (1.9)

– коэффициент Пуассона. Не умаляя общности, можем положить .

Если ввести билинейную форму , элемент и скалярное произведение , то задача З1 запишется в виде