Контрольная работа: Кручение упругопластического стержня
Составим пространство 
из построенных функций 
.
Теперь необходимо аппроксимировать множество 
, заданное формулой (1.9).
Пусть 
. Тогда 
.
Покажем, что множество 
аппроксимирует .
1) 
От противного: Пусть 
такие, что 
Но, по свойству предельной плотности
. Следовательно, 
, т.е. 
.
Отсюда, по лемме о сохранении строгих неравенств 
требуемое свойство выполнено.
2) 
слабо.
(конечномерное пространство), значит 
сильно, 
Запишем задачу З1 : найти 
такое, что 
Наряду с ней сформулируем задачу З2 :
найти 
такое, что 
При сделанных предположениях относительно 
.
4. Численный метод
Для решения задачи З2 будем использовать метод штрафа.
Исходная вариационная задача: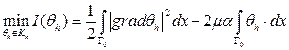 
(4.1)
Построим вспомогательный функционал
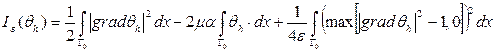(4.2)
– функция штрафа. (4.3)
, если 
, если 
Тогда вместо решения задачи (4.1) можем решать задачу 
. По свойствам функционала 
ее решение 
существует и единственно.
Кроме того, 
– выпуклая, дифференцируемая по Гато функция [2].
Производная Гато функции 
: 
Тогда задача эквивалентна решению уравнения
(4.4)
(4.5)