Контрольная работа: Методи перетворення біосигналів та аналіз медико-біологічної інформації

Сигнал – процес зміни у часі фізичного стану певного об'єкта, який можна зареєструвати, відобразити та передати.

Детерміновані сигнали – сигнали, значення яких у будь-який момент часу повністю відомі, тобто передбачувані з імовірністю, що дорівнює одиниці.

Випадкові сигнали – сигнали, значення яких у будь-який момент часу неможливо передбачити з імовірністю, що дорівнює одиниці.

Періодичним називається будь-який сигнал, для якого виконується умова

,

де період Т є кінцевим відрізком, а k – будь-яке ціле число.

Сигнали, що існують в усі моменти часу, називають аналоговими.

Послідовність чисел, що подає сигнал при цифровій обробці, називається дискретним сигналом. Числа, що складають послідовність, є значеннями сигналу в окремі (дискретні) моменти часу й називаються відліками. Переважно відліки беруть через рівні проміжки часу Т_д , що мають назву період дискретизації (або крок дискретизації). Величина, зворотна періоду дискретизації, називається частотою дискретизації

,

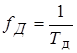відповідна їй кругова частота

.

Процес перетворення відліків сигналу в числа називається квантуванням за рівнем.

Сигнал, дискретний у часі та квантований за рівнем, називають цифровим сигналом.

Динамічним поданням називається спосіб подання сигналів, при якому реальний сигнал приблизно подається сумою деяких елементарних сигналів, що виникають у послідовні моменти часу. Якщо спрямувати до нуля тривалість окремих елементарних сигналів, то границя суми дасть точне подання вихідного сигналу.

Два сигнали u і v називають ортогональними, якщо їх скалярний добуток, а отже, і взаємна енергія дорівнюють нулю:

.

Якщо в просторі сигналів задана нескінченна система ортогональних функцій {a₁ , a₂ , …, a_n } з одиничними нормами

це означає, що в просторі сигналів заданий ортонормований базис.

Розкладання сигналу:

,

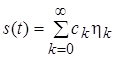де с_k – «проекції» сигналу на координатні вісі, напрямок яких задається функціями h_k (t), називається узагальненим рядом Фур'є сигналу s(t) в обраному базисі.

Сукупність коефіцієнтів ряду Фур'є {c_k } – спектр сигналу s(t).

Тригонометричний ряд Фур'є:

,

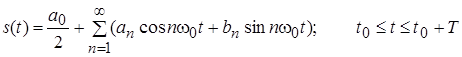де t₀ – довільна величина;

– період базисних функцій;

– кругова частота, що відповідає періоду повторення сигналу Т; частоти, кратні w₀ , що входять у формулу, називаються гармоніками;

;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--