Контрольная работа: Методы оптимизации при решении уравнений
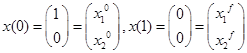 (2)
(2)
![]()
Составим функцию Лагранжа и гамильтониан:
![]()
и соответственно уравнения Эйлера-Лагранжа (здесь для Н):
![]() (3)
(3)
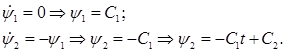 (4)
(4)
Используя замену (3), подставим выражения (4) во второе уравнение динамики в (1):
![]()
![]()
и находим общее решение
![]() (5)
(5)
Подставим его в первое уравнение (1):
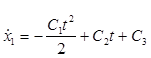
и находим общее решение:
![]() (6)
(6)
Для ![]() из (6) и
из (6) и ![]() из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1 , С2 , С3 , С4 ,:
из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1 , С2 , С3 , С4 ,:
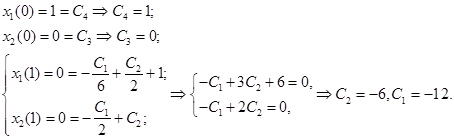
Таким образом, решение имеет вид:
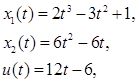
которое удовлетворяет начальным и конечным условиям.
Задание №3
Для системы, описываемой уравнениями
![]()
с заданными условиями на начальное ![]() и конечное
и конечное ![]() значение координат, найти оптимальное управление
значение координат, найти оптимальное управление ![]() , минимизирующее функционал
, минимизирующее функционал
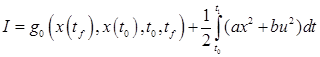
| A | B | t0 | tf | x0 | xf | g0 | a | b |
|
0 1 0 0 |
0 1 | 0 | t |
К-во Просмотров: 482
Бесплатно скачать Контрольная работа: Методы оптимизации при решении уравнений
|