Контрольная работа: Методы оптимизации при решении уравнений

Задание №1

Определить, существует ли кривая , доставляющая функционалу экстремум и, если существует, то найти ее уравнение.

Решение: Составим уравнение Эйлера и найдём его общее решение:

Используем краевые условия:

Решаем систему уравнений и получаем:

Таким образом, экстремаль имеет уравнение вида

Так как

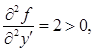
то функционал на прямой достигает минимума.

Задание №2

Найти, используя уравнение Эйлера-Лагранжа, оптимальное управление , минимизирующее функционал для системы, описываемой уравнениями

,

при начальных и конечных условиях соответственно:

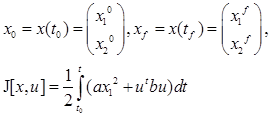
A	B	t0	tf	x0	xf	a	b
0 1 0 0	0 1	0	1	1 0	0 0	0	1

Решение

Формируем задачу по исходным данным:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--