Контрольная работа: Построение корреляции исследуемых зависимостей
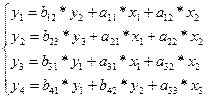
Какое это уравнение? Имеет ли оно статистическое решение с помощью КМНК?
решение
Выполним идентификацию каждого структурного уравнения и всей системы для ответа на вопрос — имеют ли решения каждое из уравнений и система в целом. Воспользуемся счетным правилом, по которому в каждом уравнении системы необходимо сравнить НY - число эндогенных переменных в данном уравнении и Dx - число отсутствующих в уравнении экзогенных переменных из общего для всей системы их перечня. Для удобства анализа представим результаты в таблице.
Таблица 3.1
Результаты идентификации структурных уравнений и всей системы
| Номер уравнения | Число эндогенных переменных в уравнении, НY | Число экзогенных переменных из общего их списка, отсутствующих в уравнении, Dx | Сравнение параметров НY и Dx +1 | Решение об идентификации уравнения |
| 1 | 2 | 1 | 2 = 1+1 | Точно идентифицируемо |
| 2 | 2 | 1 | 2 = 1+1 | Точно идентифицируемо |
| 3 | 2 | 1 | 2 = 1+1 | Точно идентифицируемо |
| 4 | 3 | 2 | 3 = 2+1 | Точно идентифицируемо |
Проверим необходимое условие идентификации для уравнений модели.
I уравнение
| Уравнение | Отсутствующие переменные | ||
| у3 | у4 | х3 | |
| Второе | b23 | 0 | 0 |
| Третье | -1 | 0 | 0 |
| Четвертое | 0 | -1 | a33 |
DetA= 0.
Следовательно, не выполняется достаточное условие идентификации, и первое уравнение не идентифицируемо.
II уравнение
| Уравнение | Отсутствующие переменные | ||
| у1 | у4 | х3 | |
| Первое | -1 | 0 | 0 |
| Третье | b31 | 0 | 0 |
| Четвертое | b41 | -1 | a33 |
DetA = 0.
Следовательно, не выполняется достаточное условие идентификации, и второе уравнение не идентифицируемо.
III уравнение
| Уравнение | Отсутствующие переменные | ||
| у2 | у4 | х3 | |
| Первое | b12 | 0 | 0 |
| Второе | -1 | 0 | 0 |
| Четвертое | b42 | -1 | a33 |
DetA = 0.
Следовательно, не выполняется достаточное условие идентификации, и третье уравнение не идентифицируемо.
IV уравнение
| Уравнение | Отсутствующие переменные | ||
| у3 | х1 | х2 | |
| Первое | 0 | а11 | а12 |
| Второе | b23 | а21 | а22 |
| Третье | -1 | а31 | а32 |
Det A =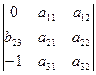 
= -a11 *
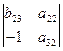+ a12 *
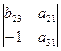¹ 0.
Ранг матрицы равен 2, что не менее числа эндогенных переменных системы без единицы.
Следовательно, выполняется достаточное условие идентификации, и четвертое уравнение точно идентифицируемо.
Вся модель является не идентифицируемой. Соответственно идентифицируемое уравнение не может быть решено с помощью КМНК.
4. Динамика ВРП на душу населения по региону характеризуется следующими данными за 1997-2003 гг. (тыс. руб.):
| 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 10,0 | 12,7 | 14,3 | 17,1 | 29,4 | 42,2 | 52,4 |
1. Определить коэффициент автокорреляции первого порядка и дать его интерпретацию.
2. Построить уравнение тренда в виде экспоненты или показательной кривой. Дать интерпретацию параметров.
3. С помощью критерия Дарбина-Уотсона сделать выводы относительно автокорреляции в остатках в рассматриваемом уравнении.
4. Дать интервальный прогноз ожидаемого уровня ВРП на душу населения на 2005 год.
5.
решение
Для изменения автокорреляции уровней динамического ряда используется коэффициент автокорреляции:
r1 =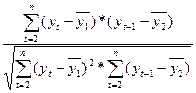 
,
где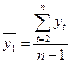 
= 
= 28,02 тыс. руб.;