Контрольная работа: Построение корреляции исследуемых зависимостей
Таблица 4.1
Расчет коэффициента автокорреляции первого порядка для временного ряда
| t | yt | yt -1 | yt -  | yt-1 -  | (yt - )*(yt-1 - ) | (yt - )2 | (yt-1 - )2 |
| 1 | 10,0 | - | - | - | - | - | - |
| 2 | 12,7 | 10,0 | -15,32 | -10,95 | 167,72 | 234,60 | 119,90 |
| 3 | 14,3 | 12,7 | -13,72 | -8,25 | 113,16 | 188,15 | 68,06 |
| 4 | 17,1 | 14,3 | -10,92 | -6,65 | 72,60 | 119,17 | 44,22 |
| 5 | 29,4 | 17,1 | 1,38 | -3,85 | -5,33 | 1,91 | 14,82 |
| 6 | 42,2 | 29,4 | 14,18 | 8,45 | 119,85 | 201,17 | 71,40 |
| 7 | 52,4 | 42,2 | 24,38 | 21,25 | 518,15 | 594,55 | 451,56 |
| Итого | 178,1 | 125,7 | 0 | 0 | 986,15 | 1339,55 | 769,98 |
r1 = 
= 0,971.
Полученное значение свидетельствует об очень тесной зависимости между ВРП на душу населения по региону текущего и непосредственно предшествующего годов и, следовательно, о наличии во временном ряде ВРП на душу населения по региону сильной линейной тенденции.
Определим параметры уравнения тренда в виде показательной кривой у = а*bt :
lgy = lga + t*lgb
Y = C + B*t,
где Y = lgy;
C = lga;
B = lgb.
Таблица 4.1
Расчет параметров тренда
| № | у | Y | t | Y*t | Y2 | t2 |
| 1 | 10,0 | 1,000 | 1 | 1,000 | 1,000 | 1 |
| 2 | 12,7 | 1,104 | 2 | 2,208 | 1,218 | 4 |
| 3 | 14,3 | 1,155 | 3 | 3,466 | 1,335 | 9 |
| 4 | 17,1 | 1,233 | 4 | 4,932 | 1,520 | 16 |
| 5 | 29,4 | 1,468 | 5 | 7,342 | 2,156 | 25 |
| 6 | 42,2 | 1,625 | 6 | 9,752 | 2,642 | 36 |
| 7 | 52,4 | 1,719 | 7 | 12,035 | 2,956 | 49 |
| Сумма | 178,1 | 9,305 | 28 | 40,735 | 12,827 | 140 |
| Среднее | 25,44 | 1,329 | 4 | 5,819 | 1,832 | 20 |
В =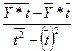 
= 
= 0,126;
А = 
- В*
= 1,329 – 0,126*4 = 0,825.
Получено линейное уравнение: 
= 0,825 + 0,126*t.
Произведем потенцирование полученного уравнения и запишем его в обычной форме: = 100,825 *100,126* t = 6,683*1,337t .
Рис. 4.1. Графическое отображение уравнения тренда.
Показатель b = 1,337 представляет собой средний за период цепной коэффициент роста уровней ряда. Параметр а = 0,825 означает начальный уровень ряда в момент времени, равный 0.
Остатки et рассчитываются по формуле:
et = yt - 
.
Критерий Дарбина-Уотсона рассчитывается по формуле:
d = 
.
Таблица 4.2
Расчет критерия Дарбина-Уотсона
| № | уt | | et | et-1 |  |  |
| 1 | 10,0 | 8,94 | 1,06 | |||
| 2 | 12,7 | 11,95 | 0,75 | 1,06 | 0,097 | 0,568 |
| 3 | 14,3 | 15,97 | -1,67 | 0,75 | 5,885 | 2,796 |
| 4 | 17,1 | 21,35 | -4,25 | -1,67 | 6,670 | 18,104 |
| 5 | 29,4 | 28,55 | 0,85 | -4,25 | 26,045 | 0,720 |
| 6 | 42,2 | 38,17 | 4,03 | 0,85 | 10,101 | 16,214 |
| 7 | 52,4 | 51,04 | 1,36 | 4,03 | 7,099 | 1,856 |
| Сумма | - | - | - | - | 55,896 | 40,258 |
d = 
= 1,39.
Фактическое значение d сравниваем с табличным значением при 5%-ном уровне значимости. При n = 7 лет и m = 1 (число факторов) нижнее значение d’ равно 0,70, а верхнее - 1,36. Так как фактическое значение d равно 1,39.
На основании схемы видно, что d = 1,39 попадает в промежуток от dU до 4 – dU . Следовательно, нет оснований отклонять гипотезу Н0 об отсутствии автокорреляции в остатках.