Контрольная работа: Расчет показателей эконометрики

Следовательно, по счетному правилу D + 1 > H(1 + 1 > 1) уравнение сверхидентифицировано.

III уравнение.

Третье уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.

Следовательно, рассматриваемая в целом структурная модель сверхидентифицируема по счетному правилу.

Проверим для каждого из уравнений достаточное условие идентификации.

Для этого составим матрицу коэффициентов при переменных модели:

Сt	Yt	Rt	Rt -1	Сt -1
I уравнение	-1	0	b11	0	b12
II уравнение	0	-1	b21	-b21	0
III уравнение	1	1	-1	0	0

В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т. е. 3-1=2.

I уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:

Уравнение	Отсутствующие переменные
	Yt	Rt -1
Второе	-1	-b21
Третье	1	0

Определитель матрицы не равен 0 (DetA = -1*0 – (1*-b₂₁ ) 0), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.

II уравнение.

Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:

Уравнение	Отсутствующие переменные
	Сt	Сt -1
Первое	-1	b12
Третье	1	0

Определитель матрицы не равен 0 (DetA = -1*0 – (1*b₁₂ ) 0.), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.

2. Первое уравнение идентифицируемое, следовательно, для его решения применяется косвенный метод наименьших квадратов.

Косвенный метод наименьших квадратов (МНК):

- Составить приведенную форму модели и определить численные значения параметров каждого уравнения системы обычным МНК.

- Путем алгебраических преобразований переходим от приведенной формы к уравнениям структурной формы модели и получаем численные оценки структурных параметров.

Для решения второго уравнения, а оно у нас сверхидентифицируемое, применяется – двухшаговый метод наименьших квадратов.

Двушшаговый метод:

- Составить приведенную форму модели и определить численные значения параметров каждого уравнения системы обычным МНК.

- Выявляем эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находим расчетные значения по соответствующим уравнениям приведенной формы модели.

- Обычным МНК определяем параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.

3. Найдем структурные коэффициенты первого и второго уравнений на основании исходных данных.

Составим расчетную таблицу (R_t = C_t + Y_t ; обозначим dR_t = R_t - R_{t -1} ).

Таблица 3.1 Расчетная таблица

№	Yt	Ct	Rt-1	Ct-1	Rt	dRt	Yt *dRt	(dRt )2	(Rt )2	(Ct-1 *Rt	Ct *Rt	(Ct-1 )2	Ct *Ct-1
1	4	14	15	12	18	3	12	9	324	216	252	144	168
2	4	13	14	11	17	3	12	9	289	187	221	121	143
3	6	15	16	12	21	5	30	25	441	252	315	144	180
4	10	20	22	15	30	8	80	64	900	450	600	225	300
5	9	20	26	17	29	3	27	9	841	493	580	289	340
6	8	14	18	12	22	4	32	16	484	264	308	144	168
7	7	16	18	14	23	5	35	25	529	322	368	196	224
8	6	12	15	10	18	3	18	9	324	180	216	100	120
9	8	12	19	11	20	1	8	1	400	220	240	121	132
10	12	21	28	20	33	5	60	25	1089	660	693	400	420
11	8	12	18	12	20	2	16	4	400	240	240	144	144
12	16	17	26	16	33	7	112	49	1089	528	561	256	272
∑	98	186	235	162	284	49	442	245	7110	4012	4594	2284	2611

Коэффициенты уравнений найдем методом наименьший квадратов:

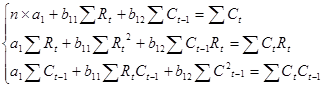
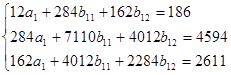
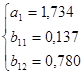(решение системы найдено в программе MATLAB)