Контрольная работа: Расчет показателей эконометрики
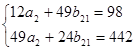
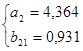
Таким образом, получена система структурных уравнений
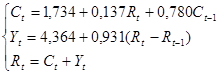
Задача 4
Динамика номинальной среднемесячной заработной платы одного работника области характеризуется следующими данными:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Тыс. руб. | 3,2 | 3,1 | 3,5 | 3,5 | 3,7 | 4,0 | 4,1 | 4,0 | 4,1 | 4,2 | 4,3 | 5,4 |
Задание
1. Определите коэффициент автокорреляции первого порядка и дайте его интерпретацию.
2. Постройте линейное уравнение тренда. Дайте интерпретацию параметрам.
3. С помощью критерия Дарбина – Уотсона сделайте выводы относительно автокорреляции в остатках в рассматриваемом уравнении.
4. Дайте интервальный прогноз ожидаемого уровня номинальной заработной платы на январь следующего года.
Решение
1. Коэффициент автокорреляции первого порядка рассчитывается по следующей формуле:
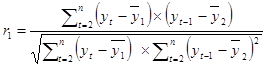
где 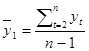 ;
; 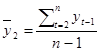
Для расчета коэффициента автокорреляции первого порядка составим расчетную таблицу:
Таблица 4.1 Расчетная таблица
| t | yt | yt-1 | |||||
| 1 | 3,2 | - | - | - | - | - | - |
| 2 | 3,1 | 3,2 | -0,9 | 2,8 | -2,5 | 7,9 | 0,8 |
| 3 | 3,5 | 3,1 | -0,5 | 2,7 | -1,3 | 7,3 | 0,2 |
| 4 | 3,5 | 3,5 | -0,5 | 3,1 | -1,5 | 9,7 | 0,2 |
| 5 | 3,7 | 3,5 | -0,3 | 3,1 | -0,9 | 9,7 | 0,1 |
| 6 | 4,0 | 3,7 | 0,0 | 3,3 | 0,0 | 11,0 | 0,0 |
| 7 | 4,1 | 4,0 | 0,1 | 3,6 | 0,4 | 13,0 | 0,0 |
| 8 | 4,0 | 4,1 | 0,0 | 3,7 | 0,0 | 13,8 | 0,0 |
| 9 | 4,1 | 4,0 | 0,1 | 3,6 | 0,4 | 13,0 | 0,0 |
| 10 | 4,2 | 4,1 | 0,2 | 3,7 | 0,8 | 13,8 | 0,0 |
| 11 | 4,3 | 4,2 | 0,3 | 3,8 | 1,2 | 14,5 | 0,1 |
| 12 | 5,4 | 4,3 | 1,4 | 3,9 | 5,5 | 15,3 | 2,0 |
| Итого | 47,1 | 41,7 | 0,0 | 37,3 | 2,1 | 129 | 3,4 |
![]() = 3,991;
= 3,991;
![]() = 0,391.
= 0,391.
Коэффициент автокорреляции первого порядка равен:
![]() =
= ![]() = 0,1.
= 0,1.
Это значение (0,1) свидетельствует о слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней, т. е. слабой зависимости между номинальной среднемесячной заработной платы текущего и непосредственно предшествующего месяца.
2. Линейное уравнение трендов имеет вид:
![]()
Параметры a и b этой модели определяются обычным МНК. Система нормальных уравнений следующая:

По исходным данным составит расчетную таблицу:
Таблица 4.2 Расчетная таблица
| t | y | yt | t2 | |
| 1 | 3,2 | 3,2 | 1 | |
| 2 | 3,1 | 6,2 | 4 | |
| 3 | 3,5 | 10,5 | 9 | |
| 4 | 3,5 | 14 | 16 | |
| 5 | 3,7 | 18,5 | 25 | |
| 6 | 4 | 24 | 36 | |
| 7 | 4,1 | 28,7 | 49 | |
| 8 | 4 | 32 | 64 | |
| 9 | 4,1 | 36,9 | 81 | |
| 10 | 4,2 | 42 | 100 | |
| 11 | 4,3 | 47,3 | 121 | |
| 12 | 5,4 | 64,8 | 144 | |
| Итого | 78 | 47,1 | 328,1 | 650 |
| Средние | 6,5 | 3,925 | 27,342 | 54,167 |
Система нормальных уравнений составит: