Контрольная работа: Розв’язання системи лінійних алгебраїчних рівнянь
![]()
дорівнює нулеві (ця сума є сумою добутків елементів ![]() -го рядка визначника на алгебраїчні доповнення другого
-го рядка визначника на алгебраїчні доповнення другого ![]() -го рядка визначника). Якщо
-го рядка визначника). Якщо ![]() сума
сума
![]()
також дорівнює нулеві, так як вона дорівнює визначнику системи ![]() , який дорівнює нулеві.
, який дорівнює нулеві.
Відмітимо, що при побудові розв’язку системи беруться алгебраїчні доповнення того рядка, де хоч би одне із ![]() не дорівнювало б нулю.
не дорівнювало б нулю.
1. Розв’язання систем лінійних рівнянь методом Жордана-Гауса
1. Основні означення та результати
Розглянемо систему m лінійних рівнянь з n невідомими:
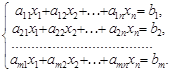 (1)
(1)
Означення . Розв’язком системи (1) називається сукупність значень невідомих
![]()
що задовольняють усі рівняння системи (1).
Означення . Система рівнянь (1) називається сумісною, якщо вона має принаймні один розв’язок, і несумісною, якщо вона не має розв’язків.
Система рівнянь називається визначеною, якщо вона має лише один розв’язок, і невизначеною, якщо вона має безліч розв’язків.
Дві системи рівнянь з однаковими невідомими називаються рівносильними, якщо кожний розв’язок однієї системи є розв’язком іншої системи або якщо ці системи рівнянь несумісні.
У результаті еквівалентних перетворень системи рівнянь завжди дістаємо рівносильну систему рівнянь. До еквівалентних перетворень системи належать:
1) переставлення місцями рівнянь;
2) множення або ділення рівнянь на число, що не дорівнює нулю;
3) додавання до деякого рівняння іншого рівняння, помноженого на довільне число.
Будь-який метод розв’язування системи рівнянь (1) передбачає виконання еквівалентних її перетворень, завдяки яким вона зводиться до такого вигляду, що розв’язок уже легко знайти.
Запишемо вектори-стовпці
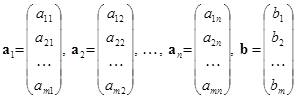 . (2)
. (2)
Для того щоб система рівнянь (1) була сумісною, тобто мала принаймні один розв’язок, необхідно і достатньо, щоб вектор ![]() був лінійною комбінацією векторів
був лінійною комбінацією векторів ![]() , тобто щоб ранг r системи векторів
, тобто щоб ранг r системи векторів ![]() дорівнював рангу розширеної системи векторів
дорівнював рангу розширеної системи векторів ![]() .
.
Звідси дістаємо умову Кронекера-Капеллі сумісності системи рівнянь.
Для того щоб система (1) була сумісною, необхідно і достатньо, щоб ранг r матриці
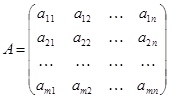 (3)
(3)
![]()
дорівнював рангу розширеної матриці
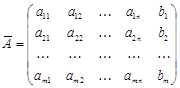 .
.
Нехай система рівнянь (1) сумісна, тобто виконується рівність