Контрольная работа: Розв’язання системи лінійних алгебраїчних рівнянь

Якщо, , то всі рівняння системи (1) лінійно незалежні. У матриці А візьмемо мінор порядку , відмінний від нуля. Цей мінор називається базисним.

Очевидно, що вибір базисного мінора неоднозначний. Якщо , то рівняння, коефіцієнти яких входять до базисного мінора, лінійно незалежні, причому решта рівнянь є лінійними комбінаціями лінійно незалежних рівнянь.

Якщо , то всі шукані змінні визначаються єдиним чином. Якщо , то змінні, коефіцієнти при яких входять до базисного мінора, називаються базисними.

Решту змінних називають вільними. Значення таких змінних можна вибирати довільно. Якщо вільні змінні вибрано, то базисні змінні можна вибрати єдиним чином. Якщо вільні невідомі дорівнюють нулю, то відповідний розв’язок системи (1) називається базисним.

Розглянемо однорідну систему рівнянь, що відповідають системі (1):

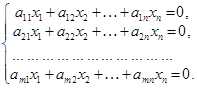(4)

Вона сумісна, бо завжди має нульовий розв’язок . Якщо , то система (4) має єдиний нульовий розв’язок. Якщо , то система (4) має лінійно незалежних ненульових розв’язків:

. (5)

Будь-яка лінійна комбінація розв’язків

(6)

також є розв’язком системи рівнянь (4).

Якщо всі розв’язки (5) лінійно незалежні, тобто ранг матриці

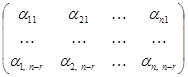
дорівнює (), то система розв’язків (5) називається фундаментальною.

Будь-який розв’язок системи рівнянь (4) можна подати у вигляді (6), тобто у вигляді лінійної комбінації розв’язків (5), які утворюють фундаментальну систему розв’язків.

При цьому розв’язок (6) системи рівнянь (4) називається загальним розв’язком однорідної системи (4). Загальний розв’язок системи (1) є сумою деякого частинного розв’язку цієї системи, наприклад базисного розв’язку, і загального розв’язку однорідної системи рівнянь (4).

Приклад. Розглянемо систему п’яти лінійних рівнянь з чотирма невідомими

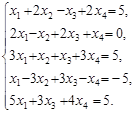(7)

Можна переконатися, що ранг матриці коефіцієнтів і ранг розширеної матриці дорівнюють r = 2. За базисний мінор візьмемо визначник

,

елементи якого входять до перших двох рівнянь і є коефіцієнтами при . Отже, базисними невідомими є , вільними невідомими - .

Замість системи (7) можна розв’язати систему, утворену з двох перших рівнянь:

(8)

Візьмемо вільні невідомі і , а далі знайдемо базисний розв’язок системи рівнянь (7): .

Вважаючи х 3 і х 4 довільними змінними, із системи рівнянь

знайдемо розв’язки

Нехай , де С 1, С 2 - довільні сталі. Тоді загальний розв’язок