Контрольная работа: Розв’язання системи лінійних алгебраїчних рівнянь

Віднімемо другий рядок від третього й запишемо таблицю

,

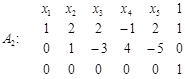яка відповідає несумісній системі рівнянь.

Система рівнянь (5) не має розв’язків. Приклад. Знайдемо розв’язок системи рівнянь:

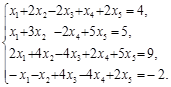(6)

Утворимо таблицю коефіцієнтів:

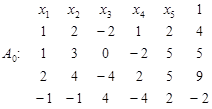
Виключивши невідомі х 1 за допомогою першого рядка, дістанемо таблицю:

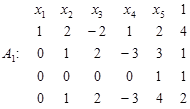
Віднявши другий і третій рядки від четвертого, дістанемо таблицю:

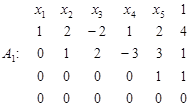
Система рівнянь сумісна, але розв’язок не є єдиним. Поміняємо місцями третій і п’ятий стовпці. Тоді маємо:

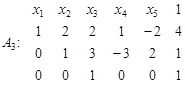
Цій таблиці відповідає система рівнянь

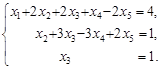
Невідомі - базисні, невідомі - вільні. Із системи рівнянь (6) знайдемо загальний розв’язок:

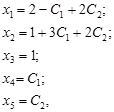
де С 1 і С 2 - довільні сталі. ·

3. Метод Жордана-Гауса

Метод Жордана-Гауса є модифікацією методу Гауса і часто застосовується в економічних розрахунках. Сутність методу полягає в тому, що кожне невідоме виключається не тільки з розміщених нижче, а з усіх рівнянь. У такому разі зростає обсяг обчислень. Якщо система n рівнянь з n невідомими

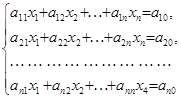(1)

має єдиний розв’язок, то вона перетворюється до вигляду

.

Приклад. Знайдемо розв’язок системи рівнянь

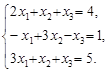
Утворимо відповідну таблицю коефіцієнтів:

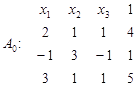
Поділивши перший рядок на 2, дістанемо таблицю:

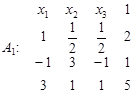
Перший рядок додамо до другого. Далі помножимо перший рядок на 3 і віднімемо від третього рядка. Утворимо таблицю: