Контрольная работа: Розв’язання системи лінійних алгебраїчних рівнянь

Зміст

Вступ

1. Розв’язання систем лінійних рівнянь методом Жордана-Гауса

2. Метод Гауса

3. Метод Жордана-Гауса

Висновки

Список використаних джерел

Вступ

При розв’язуванні системи лінійних алгебраїчних рівнянь можливі такі випадки:

а) система має єдиний розв’язок;

б) система має безліч розв’язків;

в) система не має розв’язків.

У випадках а) і б) систему називають сумісною, а у випадку в) - несумісною.

Якщо система сумісна і має єдиний розв’язок то її називають визначеною, а коли безліч розв’язків - невизначеною. Випадок, коли система має кінцеве число розв’язків більше одного неможливий.

Позначимо через матрицю системи.

.

Через позначимо матрицю, яка одержується із матриці шляхом приєднання стовпця вільних членів

.

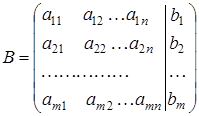Матрицю називають розширеною матрицею системи (1).

Для того, щоб система рівнянь із невідомих і рівнянь була сумісною необхідно і достатньо, щоб ранг матриці системи дорівнював рангу розширеної матриці :

.

Зауваження . У випадку сумісності системи система має єдиний розв’язок (визначена), коли і нескінченну кількість розв’язків (невизначена), коли , де - кількість невідомих.

Однорідна система лінійних рівнянь з невідомими має вигляд:

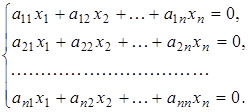
Однорідна система завжди сумісна, так як вона має розв'язок , який називається нульовим або тривіальним.

Якщо визначник системи , то тривіальний розв’язок буде єдиним розв’язком системи (3). Відмітимо, що ранг матриці системи і ранг розширеної матриці рівні.

Якщо , тоді ранг матриці системи і ранг розширеної матриці системи (3) менше числа . Припустимо, що вони дорівнюють . Тоді система (3) має нескінченну множину розв’язків

,

де - довільне дійсне число, а - алгебраїчні доповнення елементів -го рядка матриці системи. Дійсно, підставляючи ці числа в ліві частини рівнянь системи (3), одержимо:

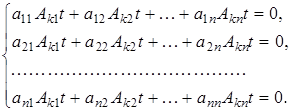
--> ЧИТАТЬ ПОЛНОСТЬЮ <--