Контрольная работа: Симплексный метод
y1 + y3 ³ 5
y1,2,3 ³ 0.
Оптимальное решение прямой задачи Х = (135; 100). Подставим его в ограничения этой задачи
3×135 + 1×100 = 505
135 < 150
100 = 100.
Условия дополняющей нежесткости (вторая теорема двойственности): для оптимальных планов двойственных задач имеют место соотношения:
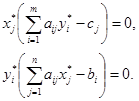
Так как для оптимального решения прямой задачи второе ограничение выполняется как неравенство, то в оптимальном решении двойственной задачи y2 = 0.
Так как для оптимального решения прямой задачи х1 > 0и х2 > 0, то оба ограничения двойственной задачи выполняются как равенство. Для нахождения решения двойственной задачи получаем систему
![]() y2 = 0
y2 = 0
3y1 + y2 = 10
y1 + y3 = 5.
Получаем решение: y1 = 10/3, y2 = 0, y3 = 5/3.
Найдем значение целевой функции двойственной задачи:
g(Y) = 505×10/3 + 150×0 + 100×5/3 = 5550/3 = 1850.
Получили gmin = fmax = 1850 ден. единиц.
Так как значения прямой и двойственной функций равны, то Y = (10/3; 0; 5/3) является оптимальным решением двойственной задачи (по первой теореме двойственности).
Задача 3.
Задание 1. Записать исходные данные задачи в виде транспортной таблицы, определить, открытой или закрытой является транспортная задача.
Задание 2. Сформулировать экономико-математическую модель исходной транспортной задачи.
Задание 3. Найти оптимальный план перевозок, отметив при этом единственность или неединственность оптимального плана.
Вариант 3.
Картофель из четырех районов должен быть перевезен в три хранилища. Запасы картофеля в районах соответственно равны 400 т, 500 т, 800 т и 500 т. Возможности хранилищ соответственно равны 700 т, 800 т и 700 т. Затраты на перевозку одной тонны картофеля из первого района в каждое из хранилищ равны соответственно 1, 4 и 3 ден. единиц; аналогичные затраты на перевозку из второго района составляют 7, 1 и 5 ден. единиц, из третьего - 4, 8 и 3 ден. единиц, из четвертого - 6, 2 и 8 ден. единиц. Найти план перевозок картофеля из районов в хранилища, при котором транспортные расходы были бы минимальными.
Решение.
Задание 1.
|
Мощности поставщиков | Мощности потребителей | ||
| 700 | 800 | 700 | |
| 400 | 1 | 4 | 3 |
| 500 | 7 | 1 | 5 |
| 800 | 4 | 8 | 3 |
| 500 | 6 | 2 | 8 |
Сумма мощностей поставщиков (запасы картофеля в всех районах) 400+500+800+500 = 2200, сумма мощностей потребителей (возможности всех хранилищ) 700+800+700 = 2200. Суммы равны, данная задача является транспортной задачей закрытого типа.