Контрольная работа: Симплексный метод
где ei -- уровни остаточной компоненты;
Модуль первого коэффициента автокорреляции сравнить с критическим уровнем этого коэффициента, значение которого принять равным 0,36;
г) нормальности закона распределения уровней остаточной компоненты на основе RS-критерия;
В качестве критических значений принять интервал от 2,7 до 3,7 (см. учебник, стр. 201—-202).
Задание 5. Оценить точность построенной трендовой линейной модели, используя показатели среднего квадратического отклонения от линии тренда (формула (5,17) учебника на с. 210, k = 1) и средней относительной ошибки аппроксимации (формула (5.14) учебника на с. 204).
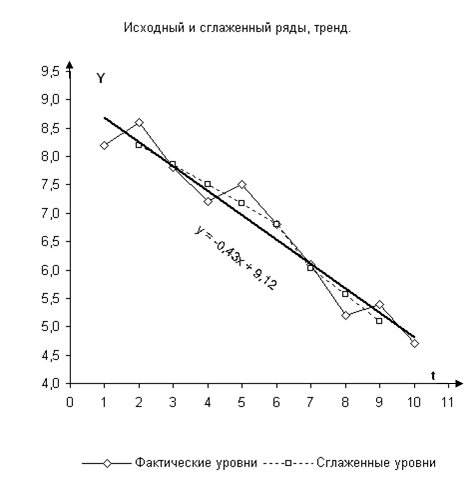
Задание 6. Построить точечный и интервальный прогноз трудоемкости производства 1 т цемента на два шага вперед (формула (5.18) учебника на с. 210). Результаты моделирования и прогнозирования отразить на графике.
Все промежуточные результаты вычислений представить в таблицах, вычисления провести с двумя десятичными знаками в дробной части.
Вариант 3. Условия при N = 3
| Текущий номер года (t) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Трудоемкость 1 т цемента (yi ) | 8,2 | 8,6 | 7,8 | 7,2 | 7,5 | 6,8 | 6,1 | 5,2 | 5,4 | 4,7 |
Решение.
Задание 1. Сглаживание ряда Y(t) произведем по простой скользящей средней
Результаты в таблице 1.
| Таблица 1. | |||
| Сглаживание ряда динамики | |||
| t | Факт Y(t) | Скользящая сумма | Скользящее среднее |
| 1 | 8,2 | - | - |
| 2 | 8,6 | 24,6 | 8,20 |
| 3 | 7,8 | 23,6 | 7,87 |
| 4 | 7,2 | 22,5 | 7,50 |
| 5 | 7,5 | 21,5 | 7,17 |
| 6 | 6,8 | 20,4 | 6,80 |
| 7 | 6,1 | 18,1 | 6,03 |
| 8 | 5,2 | 16,7 | 5,57 |
| 9 | 5,4 | 15,3 | 5,10 |
| 10 | 4,7 | - | - |
Задание 2.
Этап 1. Строим две числовые последовательности kt и lt
| t | kt | lt |
| 2 | 1 | 0 |
| 3 | 0 | 1 |
| 4 | 0 | 1 |
| 5 | 0 | 0 |
| 6 | 0 | 1 |
| 7 | 0 | 1 |
| 8 | 0 | 1 |
| 9 | 0 | 0 |
| 10 | 0 | 1 |
Этап 2. Находим величины
7; 
1 – 6 = -5.
Этап 3. Для n = 10 выпишем табличные значения m = 3,858; s1 = 1,288; s2 = 1,964.
Вычисляем
2,44; 
2,55.
Этап 4.
Так как расчетные значения ts = 2,44 и td = 2,55 больше табличного значения ta = 2,23, то в данном временном ряду присутствуют тренд и тенденция в дисперсии ряда.
Из таблицы 1 видно, что ряд Y(t) имеет тенденцию к снижению.
Задание 3. Линейную трендовую модель ищем в виде 
. Параметры модели а0 , а1 найдем, решив систему уравнений
.
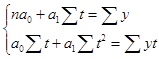n = 10.
Составим расчетную таблицу 2.
| Таблица 2 | |||
| t | y | t2 | yt |
| 1 | 8,2 | 1 | 8,2 |
| 2 | 8,6 | 4 | 17,2 |
| 3 | 7,8 | 9 | 23,4 |
| 4 | 7,2 | 16 | 28,8 |
| 5 | 7,5 | 25 | 37,5 |
| 6 | 6,8 | 36 | 40,8 |
| 7 | 6,1 | 49 | 42,7 |
| 8 | 5,2 | 64 | 41,6 |
| 9 | 5,4 | 81 | 48,6 |
| 10 | 4,7 | 100 | 47,0 |
| 55 | 67,5 | 385 | 335,8 |
Получаем систему
; 
.
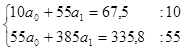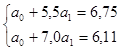