Контрольная работа: Симплексный метод
Получили трендовую модель: ![]() .
.
Задание 4.
Оценим качество модели. Для этого найдем расчетные значения Yp (t), подставляя t =1, …, 10 в трендовую модель, найдем отклонения расчетных значений от исходных E(t) = Y(t) - Yp (t). Для исследования модели на адекватность составим таблицу 3.
| Таблица 3. | |||||||||
| Расчетные величины для оценки адекватности модели | |||||||||
| t | Y(t) | Yр (t) | E(t) | k | E(t)2 | E(t)-E(t-1) | (E(t)-E(t-1))2 | E(t)*E(t-1) | IE(t)I:Y(t)*100 |
| 1 | 8,2 | 8,69 | -0,48 | 0,24 | 5,915 | ||||
| 2 | 8,6 | 8,26 | 0,35 | 1 | 0,12 | 0,83 | 0,69 | -0,17 | 4,012 |
| 3 | 7,8 | 7,83 | -0,03 | 0 | 0,00 | -0,37 | 0,14 | -0,01 | 0,321 |
| 4 | 7,2 | 7,40 | -0,20 | 1 | 0,04 | -0,17 | 0,03 | 0,00 | 2,708 |
| 5 | 7,5 | 6,97 | 0,54 | 1 | 0,29 | 0,73 | 0,53 | -0,10 | 7,133 |
| 6 | 6,8 | 6,54 | 0,27 | 0 | 0,07 | -0,27 | 0,07 | 0,14 | 3,897 |
| 7 | 6,1 | 6,11 | -0,01 | 0 | 0,00 | -0,27 | 0,07 | 0,00 | 0,082 |
| 8 | 5,2 | 5,68 | -0,48 | 1 | 0,23 | -0,47 | 0,22 | 0,00 | 9,135 |
| 9 | 5,4 | 5,25 | 0,15 | 1 | 0,02 | 0,63 | 0,40 | -0,07 | 2,87 |
| 10 | 4,7 | 4,82 | -0,12 | 0,01 | -0,27 | 0,07 | -0,02 | 2,447 | |
| S | 67,5 | 67,5 | 0,00 | 5 | 1,01 | 2,22 | -0,22 | 38,520 | |
а) Близость математического ожидания остаточной компоненты нулю.
Сумма остатков равна 0. Расчетное значение критерия Стьюдента
![]() 0.
0.
Критическое значение ta = 2,23 больше расчетного, следовательно, математическое ожидание остаточной компоненты равно нулю.
б) Проверка остатков E(t) на случайность.
Критическое количество поворотных точек для n =10 равно 2.
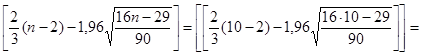 2.
2.
Для данного ряда количество таких точек k = 5. Это больше 2, поэтому остатки E(t) случайные.
в) Проверка остатков E(t) на независимость.
Независимость (отсутствие автокорреляции) проверим, используя критерий Дарбина-Уотсона:
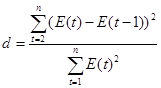 ,
, ![]() 2,20.
2,20.
d > 2, преобразуем d' = 4 - d = 4 - 2,20 = 1,80, получили 1,36 < d' = 1,80 < 2. Это означает, что остатки не зависимы.
г) Проверка остатков на соответствие нормальному закону распределения.
Используется RS - критерий:
![]() , где
, где 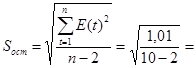 0,36.
0,36.
![]() 2,87,
2,87,
RSт = 2,7 - 3,7; так как расчетное значение RS - критерия RSрасч = 2,87 попадает внутрь интервала от 2,7 до 3,7, то остатки E(t) подчиняются по нормальному закону распределения.
Вывод: так как выполняются все условия адекватности, то модель является полностью адекватной реальному ряду экономической динамики. Ее можно использовать для построения прогнозных оценок
Задание 5.
Определим точность модели.
Среднее квадратическое отклонение от линии тренда
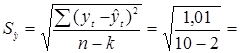 0,36.
0,36.
Средняя относительная ошибка
![]() .
.
Так как 3,85% < 5%, то точность модели высокая.
Задание 6.