Контрольная работа: Симплексный метод
![]() 4,385;
4,385; ![]() 3,955.
3,955.
Для интервального прогноза найдем ширину интервала
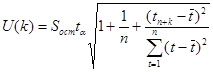 .
.
Для числа степеней свободы k = n -2 = 10 - 2 = 8 и уровня значимости a = 0,05 ta = 2,31.
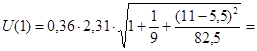 1,00;
1,00; 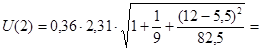 1,04.
1,04.
Границы интервалов прогноза: НГ = Yn+k - U(k), ВГ = Yn+k + U(k).
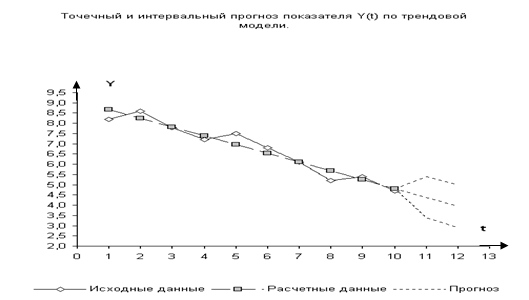
Результаты прогноза представлены таблицей 4.
| Таблица 4. | ||||
| Точечный и интервальный прогноз | ||||
| t | U(k) | Yn+k p | НГ | ВГ |
| 10 | 1,00 | 4,39 | 3,39 | 5,38 |
| 11 | 1,04 | 3,96 | 2,91 | 5,00 |
Построим график.
 |
Задача 5.
В таблице представлены первый (хij ) и второй (Yi ) квадранты схемы межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы (N — последняя цифра зачетной книжки студента):
| Потребляющие отрасли | Производящие отрасли | Конечная продукция | ||
| 1 | 2 | 3 | ||
| 1 | 200+10N | 50+10N | 300+10N | 200+10N |
| 2 | 150+10N | 250+10N | 0+10N | 100+10N |
| 3 | 230+10N | 50+10N | 150+10N | 300+10N |
Задание 1. Рассчитать объемы валовой продукции отраслей (формула (6.2) учебника на с. 237).
Задание 2. Рассчитать матрицу коэффициентов прямых затрат А = (aij ) (формула (6.4) учебника на с. 238).
Задание 3. Найти матрицу коэффициентов полных затрат B = (bij ), используя формулу (6.16) учебника на с. 244.
Задание 4. Рассчитать объемы условно чистой продукции отраслей Zj, используя формулу (6.1) учебника на с. 236.
Задание 5. Представить в таблице полную схему межотраслевого баланса (в соответствии с принципиальной схемой МОБ; табл. 6.1 учебника на с.234).
Вариант 3. Условия при N = 3.
| Таблица 1. | ||||
| Потребляющие отрасли | Производящие отрасли | Конечная продукция | ||
| 1 | 2 | 3 | ||
| 1 | 230 | 80 | 330 | 230 |
| 2 | 180 | 280 | 30 | 130 |
| 3 | 260 | 80 | 180 | 330 |
Решение.
Задание 1.
Объем валовой продукции находим по формуле
![]() .
.
Результаты в таблице 2.
| Таблица 2. | |||||
| Потребляющие отрасли | Производящие отрасли | Конечная продукция | Валовой продукт | ||
| 1 | 2 | 3 | |||
| 1 | 230 | 80 | 330 | 230 | 870 |
| 2 | 180 | 280 | 30 | 130 | 620 |
| 3 | 260 | 80 | 180 | 330 | 850 |
Задание 2.
Коэффициенты матрицы прямых затрат находим по формуле
![]()
Получаем матрицу А.
 0,26 0,26 | 0,13 | 0,39 | |
| А = | 0,21 | 0,45 | 0,04 |
| 0,30 | 0,13 | 0,21 |
Задание 3. Чтобы найти матрицу коэффициентов полных затрат В, запишем матрицу Е - А, где Е - единичная матрица.
 | 0,74 | -0,13 | -0,39 |
| Е - А = | -0,21 | 0,55 | -0,04 |
| -0,30 | -0,13 | 0,79 |
Матрица В находится по формуле
 | 1,96 | 0,70 | 1,00 |
| В = (Е - А)-1 = | 0,80 | 2,13 | 0,49 |
| 0,87 | 0,61 | 1,73 |
Задание 4. Условно чистую продукцию найдем по формуле
![]()