Контрольная работа: Симплексный метод

6

200

2

300

8 -5 v_j 1 -3 0

Исследуем этот план перевозок на оптимальность методом потенциалов. Потенциалы для занятых клеток удовлетворяют уравнениям: v_j = c_{ij +} u_i .

Пусть u₁ = 0; по клетке (1; 1) находим v₁ = 1; по клетке (3; 1) находим u₃ = -3; по клетке (4; 1) находим u₄ = -5; по клетке (4; 2) находим v₂ = -3; по клетке (3; 3) находим v₃ = -0; по клетке (2; 2) находим u₂ = -4.

Для всех клеток матрицы перевозок найдем оценки клеток d_ij = (u_i + c_ij ) - v_j :

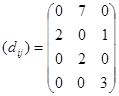
Среди оценок нет отрицательных, следовательно план перевозок Х₀ (таблица 1) оптимальный.

Так как среди оценок свободных клеток есть нулевые (клетка (1; 3)), то оптимальный план перевозок не единственный.

Общие затраты на перевозки

F(X₁ ) = 1*400 + 1*500 + 4*100 + 3*700 + 6*200 + 2*300 = 5200 ден. единиц будут минимальными при:

x₁₁ = 400, x₂₂ = 500, x₃₁ = 100, х₃₃ = 700, x₄₁ = 200, x₄₂ = 300, остальные x_ij = 0.

По оптимальному плану перевозок следует перевезти картофеля:

из первого района в первое хранилище - 400 т;

из второго района во второе хранилище - 500 т;

из третьего района в первое хранилище - 100 т,

в третье хранилище - 700 т;

из четвертого района в первое хранилище - 200 т,

во второе хранилище - 300 т.

Задача 4

В таблице приведены годовые данные о трудоемкости производства I т цемента (нормо-смен) (N —последняя цифра зачетной книжки студента):

Текущий номер года (t)	1	2	3	4	5	6	7	8	9	10
Трудоемкость 1 т цемента (yi )	7,9+0,N	8,3+0,N	7,5+0,N	6,9+0,N	7,2+0,N	6,5+0,N	5,8+0,N	4,9+0,N	5,1+0,N	4,4+0,N

Задание 1. Сгладить временной ряд методом простой скользящей средней, выбрав длину интервала сглаживания m = 3; результаты отра­зить на графике.

Задание 2. Определить наличие тренда во временном ряду методом Фостера - Стьюарта. Табличные значения статистики Стьюдента t_a принять равными при уровне значимости a = 0.05 t_a = 2,23 , а при a = 0,30 - t_a = 1,09; другие необходимые табличные данные приведены в таблице 4.5 учебника на с.153 (описание метода Фостера - Стьюар­та см. учебник с. 151- 153).

Задание 3. Для исходного временного ряда построить линейную трендовую модель , определив ее параметры на основе метода наименьших квадратов (соответствующую систему нормальных уравнений см. в учебнике на с. 196 формула (5.5)).

Задание 4. Оценить адекватность построенной модели на основе исследования

а) близости математического ожидания остаточной компоненты (ряда остатков) нулю; критические значения r-критерия принять равным тому числу, как указанно в задании 2;

б) случайности отклонений остаточной компоненты по критерию пиков (поворотных точек); Расчеты выполнить на основе соотношения 5.9. учебника на с. 200;

в) независимости уровней ряда остатков (отсутствие автокорреляции) на основе критерия Дарбина — Уотсона (см. учебник с. 203— 204), используя в качестве критических значений d_l = 1.08 и d₂ = 1,36; если критерий Дарбина — Уотсона ответа не дает, исследование независимости провести по первому коэффициенту автокорреляции: