Контрольная работа: Сопротивление материалов

где ммм – ширина прямоугольного сечения балки;

ммм – высота прямоугольного сечения балки;

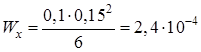м³ ;

– допускаемые напряжения при изгибе; для дерева принимаем МПа.

Проверяем несущую способность деревянной балки

ПаМПа,

что значительно больше допускаемых напряжений. Следовательно, несущая способность балки не соблюдается.

Ответ : Прочность балки недостаточна.

Задача 5

Для двухопорной балки подобрать сечение двутавра из условия прочности.

Проверить прочность по касательным напряжениям. Построить эпюры и для сечений, в которых и . Нагрузку принять состоящей: 1) из 80% постоянной, коэффициент перегрузки 2) из 20% временной, коэффициент перегрузки .

Данные для задачи своего варианта взять из табл. 5 и схемы на рис. 12.

Таблица 5

Вариант			, кН/м	, кН∙м
	м
49	4	4	12	6

Решение

1. Определяем действительные значения нагрузок, действующих на балку, используя метод расчета предельного состояния по несущей способности.

При этом расчетное усилие в балке (в нашем случае и ) определяем как сумму усилий от каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих каждой нагрузке коэффициентов перегрузки. В результате получим

кН∙м;

кН/м.

2. Выполняем расчетную схему согласно исходных данных (рис.6,а).

Отбросим опоры и заменим их влияние на балку опорными реакциями и (рис.6, б). Учитывая симметричность конструкции, получим

кН.

2. Балка имеет три участка. Обозначим через расстояние от левого или правого концов балки до некоторого его сечения. Составим выражения для поперечных сил и изгибающих моментов , возникающих в поперечных сечениях балки и по ним установим значения ординат эпюр в ее характерных сечениях.

Участок I :

;

.

При

кН;

кН∙м.