Контрольная работа: Теорія і практика обчислення визначників

ТЕОРІЯ І ПРАКТИКА ОБЧИСЛЕННЯ ВИЗНАЧНИКІВ

1. Основні поняття і теореми

Def. Нехай задано квадратну матрицю А n-го порядку з елементами a_ij , де i визначає номер рядка, j – номер стовпця і при цьому через х_j позначені стовпці матриці А, тобто

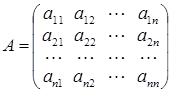і .

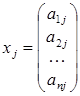Визначником(det A)квадратної матриці А зі стовпцями х_j називається функціонал j(х₁ , х₂ , … , х_n ) щодо стовпців цієї матриці, який:

а) лінійний за кожним з аргументів (полілінійний):

теорема обчислення визначник сума

j(х₁ , …, aх_i1 + bх_i2 , … , х_n ) = aj(х₁ , … , х_i1 , … , х_n ) + bj(х₁ , … , х_i2 , … , х_n );

б) абсолютно антисиметричний (антисиметричний по будь-якій парі аргументів): j(х₁ , … , х_i , … , х_j , … , х_n ) = –j(х₁ , … , х_j , … , х_i , … , х_n );

в) підкоряється умові нормування:

.

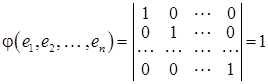Тоді, з огляду на загальний вигляд полілінійного антисиметричного функціонала, маємо:

а б

Рис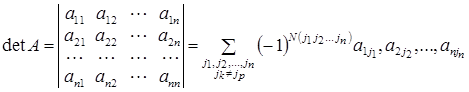. 1

, (1)

де N(j₁ j₂ … j_n ) – кількість безладів у перестановці .

Говорять, що в перестановці мається безлад, якщо j_k > j_m і k < m.

З формули (1) для визначника другого порядку одержуємо .

Визначниктретього порядку дорівнює сумі шести (3! = 6) доданків. Для побудови цих доданків зручно скористатися правилом трикутників.Добуток елементів, що розташовані на головній діагоналі, а також добутки елементів, що є вершинами двох трикутників на рис. 1а, беруться з множником +1, а добуток елементів, що розташовані на побічній діагоналі, а також добутки елементів, що є вершинами двох трикутників на мал. 1б, беруться з множником –1, тобто

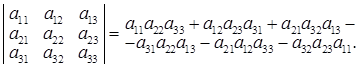
Властивості визначників:

1°. det A = det A^T . З цієї властивості випливає, що рядки і стовпці визначника рівноправні. У силу цього всі властивості, сформульовані для стовпців, можуть бути сформульовані і для рядків визначника.

2°. Якщо один зі стовпців визначника складається з нульових елементів, то визначник дорівнює нулю.

3°. Загальний множник у стовпці визначника можна виносити за знак визначника.

4°. Якщо у визначнику поміняти два стовпці місцями, то визначник змінить знак.

5°. Визначник, що має два рівних стовпці, дорівнює нулю.

6°. Якщо стовпці визначника лінійно залежні, то визначник дорівнює нулю.

7°..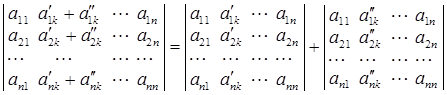

--> ЧИТАТЬ ПОЛНОСТЬЮ <--