Контрольная работа: Теорія і практика обчислення визначників
20. Обчислити наступні визначники 4-го порядку:
а) 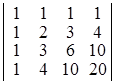 ; б)
; б) 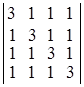 ;
;
в) 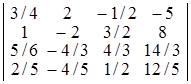 ; г)
; г) 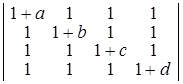 .
.
Dа) 1; б) 48; в) 1; г) 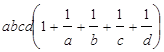 . ▲
. ▲
21. Обчислити визначники 4-го порядку:
а) 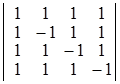 ; б)
; б) 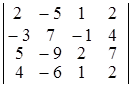 ; в)
; в) 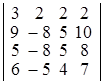 ; г)
; г) 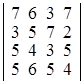 .
.
Dа) –8; б) –9; в) –6; г) –10. ▲
22. Обчислити визначники 5-го порядку:
а) 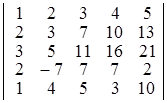 ; б)
; б) 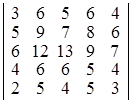 . Dа) 52; б) 5. ▲
. Dа) 52; б) 5. ▲
23. Зведенням до трикутного вигляду обчислити визначники:
а) 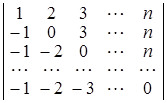 ; б)
; б) 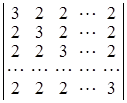 ;
;
в) 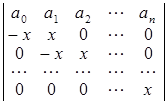 ; г)
; г) 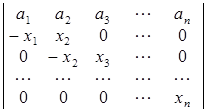 .
.
D а) n!; б) 2n + 1; в) хn (а0 + а1 + … + аn ); г) ![]() . ▲
. ▲
24. Обчислити визначники методом виділення лінійних множників:
а) 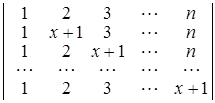 ; б)
; б) 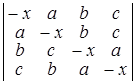 ;
;
в) 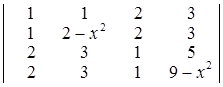 ; г)
; г) 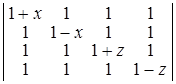 .
.
D а) (х – 1)(х – 2)…(х – n +1); б) (x – a – b – c)(x – a + b + c)(x + a – b + c)(x + a + b – c);
в) (х2 – 1)(х2 – 4); г) x2 z2 , вказівка: визначник не зміниться, якщо 1-й стовпець поміняти місцями з 2-м стовпцем і одночасно 1-й рядок із 2-м рядком; при х = 0 визначник дорівнює 0, аналогічно по z. ▲
25. Розв’язати рівняння:
а) 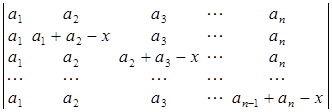 ; б)
; б) 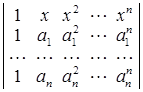 ;
;
в)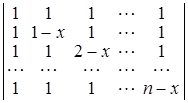 ; г)
; г) 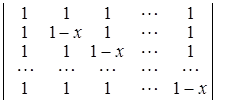 (х ÎR).
(х ÎR).
D а) хi = ai , i = 1, 2, … , n – 1; б) хi = ai , i = 1, 2, … , n; в) х = 0, 1, 2, … , n – 1; г) x = 1. ▲
26. Використовуючи метод рекурентних співвідношень, обчислити визначники: а) 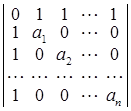 ; б)
; б) 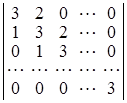 ; в)
; в) 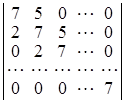 .
.
D а) ![]() ; б) 2n + 1 – 1; в)
; б) 2n + 1 – 1; в) ![]() . ▲
. ▲
27. Обчислити визначники методом представлення їх у вигляді суми визначників:
а) 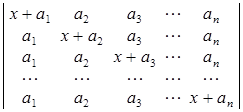 ; б)
; б) 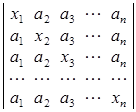 .
.
∆ а) хn + (а1 + а2 + … + аn )хn – 1 ; б) вказівка: xi º (xi – ai + ai ),
![]() . ▲
. ▲
28. Обчислити визначники методом зміни елементів визначника: