Контрольная работа: Теорія і практика обчислення визначників

9°. Визначник добутку двох квадратних матриць n-го порядку дорівнює добуткові визначників цих матриць.

Def. Якщо в матриці А порядку n викреслити i-й рядок та j-й стовпець, то елементи, що залишилися, утворять матрицю (n – 1)-го порядку. Її визначник називається мінором (n – 1)-го порядку, додатковим до елемента a_ij матриці А, і позначається М_ij , а величина А_ij = (–1) ^{i + j} М_ij називається алгебраїчним доповненням до елемента a_ij матриці А.

10°.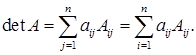 (Розкриття визначника за елементами j-го стовпця та за елементами i-го рядка).

11°.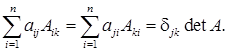

12°. (Теорема Лапласа).

.

Тут – мінор, складений з елементів матриці А, що розташовані на перетині рядків i₁ , i₂ , …, i_k і стовпців j₁ , j₂ , …, j_k , а – алгебраїчне доповнення до цього мінора.

13°. (Про зміну елементів визначника).

Якщо , а , то .

3. Приклади розв’язування задач

Задача 1. Обчислити визначник: .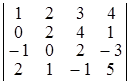

Розв’язання. I спосіб. Обчислимо визначник розкладанням за елементами (наприклад) третього рядка (властивість 10º):

.

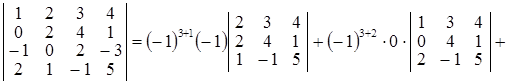
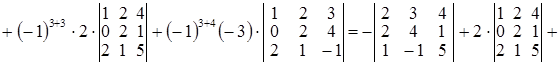
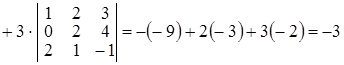Визначники третього порядку, що входять до останнього виразу, обчислені за правилом трикутників.

II спосіб. Обчислимо визначник розкладанням за мінорами 2-го порядку (наприклад тими, що розташовані в 1-муі 2-мурядках вихідного визначника, властивість 12º). Усього таких мінорів буде шість (1-й, 2-й стовпці; 1-й, 3-й стовпці; 1-й, 4-й стовпці; 2-й, 3-й стовпці; 2-й, 4-й стовпці; 3-й, 4-й стовпці). Одержимо:

.

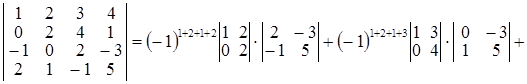
III спосіб. Обчислимо визначник методом приведення визначника до трикутного вигляду. Для цього скористаємося властивістю 8°.

а) 1-й рядок додамо до 3-го рядка;

б) 1-й рядок, помножений на (–2), додамо до 4-горядка.

При цьому визначник не зміниться.

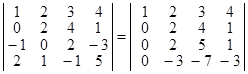
Далі: в) від 1-го рядка віднімемо 2-й рядок;

г) 2-й рядок, помножений на 3, додамо до 4-го рядка, помноженого на 2. При цьому визначник збільшиться вдвічі за рахунок множення 4-го рядка на 2.

;
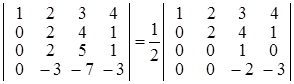