Контрольная работа: Застосування сплайн-функцій до розв’язування задач інтерполяції

– знайти і опрацювати літературу із даної теми;

– систематизувати опрацьований матеріал;

– отримати формули для розрахунків інтерполяційних задач;

– визначити практичність кубічних В-сплайнів в порівнянні з іншими сплайнами і В-сплайнами;

1 B -сплайни

1.1 Базис із В-сплайнів

Одним з найширше використовуваних представлень кривих в комп'ютерному баченні є представлення у вигляді В-сплайну. Важливо розрізняти сплайни і В-сплайни. В-сплайни є поліноміальними функціями. Сплайни є лінійною комбінацією В-сплайнів. У літературі сплайни зазвичай визначаються як різні види степеневої функції. Для обчислень зручніше визначати сплайни рекурсивними функціями.

Приймемо без доведення наступну лему, яку буде використано для доведення важливої теореми:

Лема 1 . Нехай - множина сплайнів порядку m дефекту1 порозбиттю. Якщо і сплайн із задовольняє умови, то на .

Теорема 1 . Системаіз В-сплайнів

, (1) порядку за розбитям з носіямиєбазисом в .

Доведення. Нехай

, ; (2) потрібнодовести,що ().Безпосередньо із визначенняВ-сплайнів (1)виплива, що при ;але тоді з урахуванням(2)

, ів силулеми1 для . Таким чином,

, .(3)

Оскількинапроміжку, а при , тоіз(3)слідує,що, такщо

, .

Для при і при , а тому і

, .

Розмірковуючи аналогічно,далі прийдемодорівності

що йтребабулодовести.

Наслідок 1. Будь-якийсплайн із єдиним чином представляється у вигляді

, .(4)

Якщо сплайн із однозначно визначається деяким набором із інтерполяційних умов, то, підставляючи в ці умови замість суму (4), отримаємо систему лінійних рівнянь для визначення коефіцієнтів . Усилу скінченності носіїв сплайнів в кожному рядочку визначника цієї системи, не дорівнюватимуть нулю лише елементів - значення сплайнів (або їх похідних) в одній із точок розбиття . При цьому не нульові елементи, які відповідають внутрішнім умовам інтерполяції, будуть розміщені вздовж головної діагоналі визначника. Саме це і забезпечує, принаймні для малих , простоту обчислення коефіцієнтів лінійної комбінації (4) [1].

1.2 В-сплайн нульового степеня та рекурентна форма запису В-сплайнів вищих порядків

В-сплайном нульового степеня , побудованим на числовій прямій по розбиттю , називається функція вигляду:

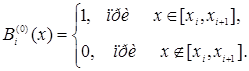, (5)

Єдине обмеження полягає в тому, що В-сплайни повинні відповідати умові: