Контрольная работа: Застосування сплайн-функцій до розв’язування задач інтерполяції

В-сплайн степеня , побудований на числовій прямій по розбиттю , визначається наступною рекурентною формулою:

, (6)

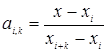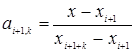де , . (7)

При однаковій відстані між сусідніми вузлами В-сплайни називаються однорідними , в протилежному випадку неоднорідними . Для однорідних B-сплайнів, базисні B-сплайни однакового степеня є зміщеними екземплярами однієї функції [3].

Нерекурсивним визначенням базисних B-сплайнів є

, (8)

де , 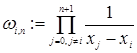[3]. (9)

1.3 Лінійні B-сплайни

Лінійні B-сплайни є неперервними, але не диференційованими.

Скориставшись рекурентною формулою (6), отримаємо формулу для лінійного В-сплайна:

(10)

Підставивши у (10) формулу (5) маємо:

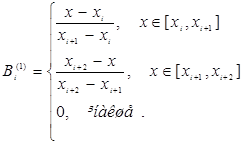
(11)

Або у випадку рівномірної сітки з кроком () отримаємо:

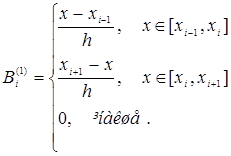
(11’)

Нижче на малюнку 1 представлено графік В-сплайна 1-го порядку:

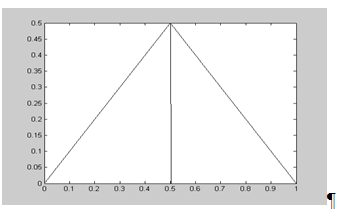
Мал. 1 - Графік В-сплайна

1.4 К вадратичні B-сплайни

Із рекурентної формули (6), отримаємо наступну форму запису квадратичного В-сплайна:

(12)

Тепер ми можемо, або скористатись лише формулою (11), підставивши її у (12) отримаємо:

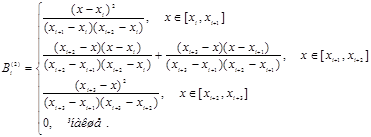
(13)

А у випадку рівномірної сітки з кроком h матимемо:

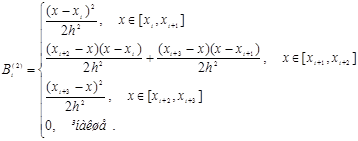(13’)

Або спершу в (12) підставимо (10) і, зробивши відповідні перетворення, отримаємо квадратичний В-сплайн в вигляді:

, (14)

а потім в (14) підставимо (5) і отримаємо ту ж саму формулу (13) [4].

Графік В-сплайна 2-го - - степеня представлено на малюнку 2: