Контрольная работа: Застосування сплайн-функцій до розв’язування задач інтерполяції
, ![]() (33) де
(33) де
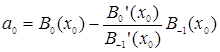 ,
, 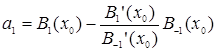 ,
,
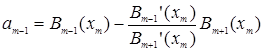 ,
,  ,(34)
,(34)
 ,
,  .
.
Розв’язавши систему (33), знайдемо коефіцієнти ![]() , для шуканого сплайна:
, для шуканого сплайна:
![]()
(де у нашому випадку ![]() ).
).
Отже необхідно знайти і підставити відповідні значення та розв’язати матричне рівняння:
![]() ,
,
де ![]() - тридіагональна матриця, а
- тридіагональна матриця, а ![]() - шуканий вектор коефіцієнтів.
- шуканий вектор коефіцієнтів.
Для нашої функції ![]() маємо наступні дані:
маємо наступні дані:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Тоді три діагональна матриця ![]() і вектор
і вектор ![]() відповідно дорівнюватимуть:
відповідно дорівнюватимуть:
 ,
,  ,
,
підставивши їх у матричне рівняння, отримаємо вектор ![]() :
:
![]() ,
,
 ,
, .
.
Отже, маємо інтерполяційний сплайн функції ![]() на проміжку
на проміжку ![]() :
:

Побудуємо його графік (в середовищі Matlab):

Мал. 4, 5 – Графіки функції